Question

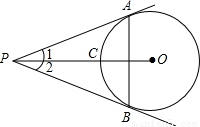
如图所示，PA切⊙O于点A，且PO=6，若图中阴影部分的面积为

9

2

3

-

3

2

π，则∠P=

30°

．

Answer 1

分析：连接OA，设OA=x，AP=y，由AP为圆O的切线，利用切线的性质得到OA与AP垂直，在直角三角形AOP中，利用勾股定理列出关系式，再由阴影部分的面积由直角三角形AOP的面积减去扇形的面积，表示出阴影部分面积等于已知的面积，可得出关于x与y的另一个关系式，联立两关系式求出x与y的值，可得出OA等于OP的一半，利用直角三角形中一直角边等于斜边的一半，此直角边所对的角为30°即可求出∠P的度数．

解答：解：连接OA，设OA=x，AP=y，
∵AP为圆O的切线，
∴OA⊥AP，
在Rt△OAP中，根据勾股定理得：OA²+AP²=OP²，即x²+y²=36②，
∵S_阴影=S_△AOP-S_扇形=

1

2

xy-

nπx2

360

=

9

2

3

-

3

2

π，
∴xy=9

3

②，
联立①②解得：x=3，y=3

3

，
∴OA=

1

2

OP，
∴∠P=30°．
故答案为：30°

点评：此题考查了切线的性质，勾股定理，扇形面积公式，以及直角三角形的性质，熟练掌握定理及性质是解本题的关键．