题目内容
如图，为了测量河的宽度，东北岸选了一点A，东南岸选相距200m的B、C两点测得∠ABC=60°，∠ACB=45°，求这段河的宽度．（精确到0.1m）
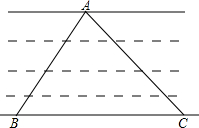
解：过A作AD⊥BC于D，
在Rt△ADB中，∠B=60°，
∴∠BAD=30°，
∴BD=AD•tan30°=
AD，
在Rt△ADC中，∠C=45°，
∴CD=AD，又BC=200，
∴BD+CD=AD+AD=200．
解得AD≈126.8（米）．
分析：过A作AO⊥BC于D，根据∠ABC=60°，∠ACB=45°即可求出BD、CD与AD关系，根据BC=200m，可以求得AD的长度，即可解题．
点评：本题考查了特殊角的三角函数值的计算，三角函数值在直角三角形中的灵活应用．
在Rt△ADB中，∠B=60°，
∴∠BAD=30°，
∴BD=AD•tan30°=
AD，在Rt△ADC中，∠C=45°，
∴CD=AD，又BC=200，
∴BD+CD=
AD+AD=200．解得AD≈126.8（米）．
分析：过A作AO⊥BC于D，根据∠ABC=60°，∠ACB=45°即可求出BD、CD与AD关系，根据BC=200m，可以求得AD的长度，即可解题．
点评：本题考查了特殊角的三角函数值的计算，三角函数值在直角三角形中的灵活应用．
练习册系列答案
名校课堂系列答案
相关题目
如图，为了测量河宽AB（假设河的两岸平行），测得∠ACB=30°，∠ADB=60°，CD=60m，则河宽AB为
如图，为了测量河宽，在河的一边沿岸选取A、B两点，对岸岸边有一块石头C．在△ABC中，测得∠A=60°，∠B=45°，AB=60米．
如图，为了测量河宽，某同学采用的办法是：在河的对岸选取一点A，在河的这岸选一点B，使AB与河的边沿垂直，然后在AB的延长线上取一点C，并量得BC=30米；然后又在河的这边取一点D，并量得BD=20米；最后在射线AD上取一点E，使得CE∥BD．按照这种做法，她能根据已有的数据求出河宽AB吗？若能，请求出河宽AB；若不能，她还必须测量哪一条线段的长？假设这条线段的长是m米，请你用含m的代数式表示河宽AB．