题目内容
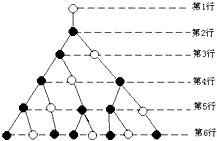
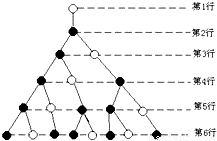
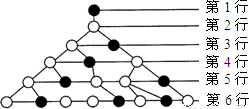
 18、如图是一个树形图的生长过程,根据图中所示的生长规律,第12行的空心圆点的个数是
18、如图是一个树形图的生长过程,根据图中所示的生长规律,第12行的空心圆点的个数是39
.分析:根据图示可以看出:一个空心圆点到了下一行变成一个实心圆点和一个空心圆点,一个实心圆点到了下一行变成一个空心圆点,在树形图中这些数字每一个都等于前面两个数之和,它们正好构成了斐波那契数列.
解答:解:如果将第一行中的1个实心圆点和0个空心圆 点用数对(1,0)表示,将第二行中的0个实心圆点和1个空心圆点用数对(0,1)表示,
则第三、四、五行…的实心圆点和空心圆点分别可用数对(1,1),(1,2),(2,3)…表示,
根据上述得出的变化规律可知:后行数对的第二个数是前一行数对中的两数之和,第一个数是前一行数对中的第二个数,
据此可以推算出第12行的数对为(39,105).
∴第十二行的实心圆点的个数等于39个.
故答案为:39.
则第三、四、五行…的实心圆点和空心圆点分别可用数对(1,1),(1,2),(2,3)…表示,
根据上述得出的变化规律可知:后行数对的第二个数是前一行数对中的两数之和,第一个数是前一行数对中的第二个数,
据此可以推算出第12行的数对为(39,105).
∴第十二行的实心圆点的个数等于39个.
故答案为:39.
点评:本题考查了图形的规律变化,得到第n行实心球的个数与前2行实心球个数的关系是解决本题的关键,难度适中.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
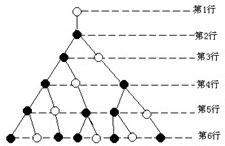 7、如图是一个树形图的生长过程,依据图中所示的生长规律,第15行的实心圆点的个数等于
7、如图是一个树形图的生长过程,依据图中所示的生长规律,第15行的实心圆点的个数等于