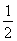题目内容
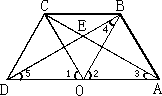
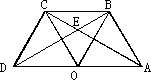
如图,O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形ODC,连接AC、BD,相交于点E,连接BC.求∠AEB的大小.
答案:
解析:
解析:
|
解:如图,因为△DOC和△AOB都是等边三角形,且O是线段AD的中点, 所以OD=OC=OB=OA,∠1=∠2=60°.所以∠4=∠5. 又因为∠4+∠5=∠2=60°,所以∠4=∠5=30°. 同理∠3=30°. 所以∠AEB=∠5+∠3=30°+30°=60°.
|

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
如图,B是线段AD的中点,C是BD上一点,则下列结论中错误的是( )
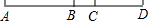
| A、BC=AB-CD | ||
B、BC=(
| ||
C、BC=
| ||
| D、BC=AC-BD |