题目内容
已知x=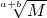 是M的立方根,y=
是M的立方根,y= 是x的相反数,且M=3a-7,那么x的平方根是________.
是x的相反数,且M=3a-7,那么x的平方根是________.
±
分析:由于x=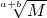 是M的立方根,所以a+b=3 ①,而y=
是M的立方根,所以a+b=3 ①,而y= 是x的相反数,所以M=-(b-6),而M=3a-7,代入M=-(b-6),得3a-7=-(b-6)②,联立①②解方程组即可求出a、b,然后就可以求出x的平方根.
是x的相反数,所以M=-(b-6),而M=3a-7,代入M=-(b-6),得3a-7=-(b-6)②,联立①②解方程组即可求出a、b,然后就可以求出x的平方根.
解答:∵x=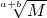 是M的立方根,
是M的立方根,
∴a+b=3,①
∵ 是x的相反数,
是x的相反数,
∴M=-(b-6),
而M=3a-7,代入M=-(b-6),
得3a-7=-(b-6)②,
联立①②得: ,
,
解之得: ,
,
∴M=3a-7=8,
∴x=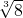 =2,
=2,
∴x的平方根是± .
.
故答案为:± .
.
点评:此题主要考查了立方根、平方根、相反数的定义和性质,解题的关键利用题目的已知条件得到关于a、b的方程组,解方程组即可解决问题.

分析:由于x=
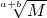 是M的立方根,所以a+b=3 ①,而y=
是M的立方根,所以a+b=3 ①,而y= 是x的相反数,所以M=-(b-6),而M=3a-7,代入M=-(b-6),得3a-7=-(b-6)②,联立①②解方程组即可求出a、b,然后就可以求出x的平方根.
是x的相反数,所以M=-(b-6),而M=3a-7,代入M=-(b-6),得3a-7=-(b-6)②,联立①②解方程组即可求出a、b,然后就可以求出x的平方根.解答:∵x=
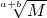 是M的立方根,
是M的立方根,∴a+b=3,①
∵
 是x的相反数,
是x的相反数,∴M=-(b-6),
而M=3a-7,代入M=-(b-6),
得3a-7=-(b-6)②,
联立①②得:
 ,
,解之得:
 ,
,∴M=3a-7=8,
∴x=
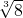 =2,
=2,∴x的平方根是±
 .
.故答案为:±
 .
.点评:此题主要考查了立方根、平方根、相反数的定义和性质,解题的关键利用题目的已知条件得到关于a、b的方程组,解方程组即可解决问题.

练习册系列答案
相关题目
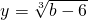 是x的相反数,且M=3a-7,求x的平方根.
是x的相反数,且M=3a-7,求x的平方根.