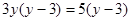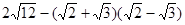题目内容
(每小题4分共12分)探索与思考(1)观察下列式子:
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
根据这些等式的特点,你能用式子表示它的一般规律吗能,请写出.
(2)观察下列等式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
想一想:等式左边各项幂的底数与右边幂的底数有什么关系答:
试一试:13+23+33+43+…+203=
猜一猜:可引出什么规律:(可用带字母的等式表示,也可用文字叙述).
分析:根据题意的数列可知规律是:(1)
×(n+1)=
+(n+1);(2)通过观察了可知等式左边各项幂的底数和等于右边幂的底数;总结规律即可.
| n+1 |
| n |
| n+1 |
| n |
解答:解:根据分析可得:(1)
×(n+1)=
+(n+1);
(2)13+23+33+43+…+203=2102;
等式左边各项幂的底数和等于右边幂的底数;
(1+2+3+…+20)2=2102;
规律为:13+23+…+n3=(1+2+…+n)2=[
]2.
| n+1 |
| n |
| n+1 |
| n |
(2)13+23+33+43+…+203=2102;
等式左边各项幂的底数和等于右边幂的底数;
(1+2+3+…+20)2=2102;
规律为:13+23+…+n3=(1+2+…+n)2=[
| n(n+1) |
| 2 |
点评:主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
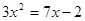 (2)
(2)
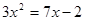 (2)
(2)