题目内容
【题目】如图①,AB是⊙O的直径,且AB=10,C是⊙O上的动点,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.(1)求证:∠DAC=∠BAC;
(2)若AD和⊙O相切于点A,求AD的长;
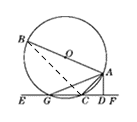
(3)若把直线EF向上平行移动,如图②,EF交⊙O于G,C两点,题中的其他条件不变,试问这时与∠DAC相等的角是否存在,并说明理由.

【答案】(1)详见解析;(2)5;(3)存在,∠BAG=∠DAC,理由详见解析.
【解析】试题分析:
(1)连接OC,则OC∥AD,得∠OCA=∠DAC,又∠OCA=∠OAC,即可证明;
(2)根据切线长定理,证明矩形OADC是正方形;
(3)连接BC,证∠BCG=∠DAC,又∠BCG=∠BAG,即得证.
试题解析:
(1)证明:如图①,连接OC.∵直线EF和⊙O相切于点C,
∴OC⊥EF.∵AD⊥EF,∴OC∥AD.∴∠DAC=∠OCA.
∵OA=OC,∴∠BAC=∠OCA.∴∠DAC=∠BAC.
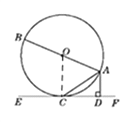
(2)解:∵AD和⊙O相切于点A,∴OA⊥AD.∵AD⊥EF,OC⊥EF,
∴∠OAD=∠ADC=∠OCD=90°.∴四边形OADC是矩形.∵OA=OC,
∴矩形OADC是正方形.∴AD=OA.∵AB=2OA=10,∴AD=OA=5.
(3)解:存在,∠BAG=∠DAC.理由如下:如图,连接BC.∵AB是⊙O的直径,
∴∠BCA=90°.∴∠ACD+∠BCG=90°.∵∠ADC=90°,
∴∠ACD+∠DAC=90°.∴∠DAC=∠BCG.∵∠BCG=∠BAG,∴∠BAG=∠DAC.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如下表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,
=8, ![]() =1.8.根据上述信息完成下列问题:
=1.8.根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整.
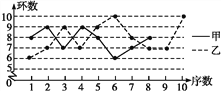
(2)求乙运动员射击训练成绩的众数和中位数.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.