题目内容
 一个零件的形状如图所示,工人师傅量得这个零件的各边尺寸(单位:dm)如下:
一个零件的形状如图所示,工人师傅量得这个零件的各边尺寸(单位:dm)如下:AB=3,AD=4,BC=12,CD=13,且∠DAB=90°,求这个零件的面积.
分析:连接BD后,根据勾股定理和勾股定理逆定理的应用,可判断这个四边形是由两个直角三角形组成,从而可求出面积.
解答: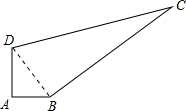 解:连接BD,
解:连接BD,
∵AB=3,AD=4,∠DAB=90°,
∴BD=
=
=5,
∵BC=12,CD=13,
∴BD2+BC2=CD2,
∴∠DBC=90°.
∴四边形ABCD的面积=
×3×4+
×5×12=36.
这个零件的面积是36平方分米.
 解:连接BD,
解:连接BD,∵AB=3,AD=4,∠DAB=90°,
∴BD=
| AD2+AB2 |
| 42+32 |
∵BC=12,CD=13,
∴BD2+BC2=CD2,
∴∠DBC=90°.
∴四边形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
这个零件的面积是36平方分米.
点评:本题考查勾股定理的应用,和勾股定理逆定理的应用,先用勾股定理求出边长,再用勾股定理的逆定理判断出是直角三角形,从而可求出面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 28、一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠D应分别是20°和30°.
28、一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠D应分别是20°和30°.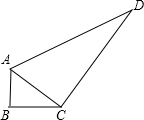 一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗? 23、一个零件的形状如图所示,按规定∠A=100°,AB与CD,AF与DE的夹角分别是32°和22°,若检查员量得∠CDE=150°,能判定这个零件合格吗?请说明理由.
23、一个零件的形状如图所示,按规定∠A=100°,AB与CD,AF与DE的夹角分别是32°和22°,若检查员量得∠CDE=150°,能判定这个零件合格吗?请说明理由.
 21、一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是30°和20°,李叔叔量得∠BDC=142°,就判定这个零件不合格,你能说出其中的道理吗?
21、一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是30°和20°,李叔叔量得∠BDC=142°,就判定这个零件不合格,你能说出其中的道理吗?