【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
【答案】(1)A种型号的衣服每件90元,B种型号的衣服100元;(2)有三种进货方案,具体见解析.
【解析】试题分析:(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利不少于699元,且A型号衣服不多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
试题解析:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则: ,
,
解之得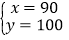 .
.
答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得: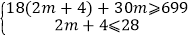 ,
,
解之得192m12,
∵m为正整数,
∴m=10、11、12,2m+4=24、26、28.
答:有三种进货方案:
(1)B型号衣服购买10件,A型号衣服购进24件;
(2)B型号衣服购买11件,A型号衣服购进26件;
(3)B型号衣服购买12件,A型号衣服购进28件。
点睛:点睛:本题主要考查二元一次方程组和一元一次不等式组的实际问题的应用,解题的关键是读懂题目的意思,根据题目给出的条件,设出未知数,分别找出甲组和乙组对应的工作时间,找出合适的等量关系,列出方程组,再求解.
【题型】解答题
【结束】
21
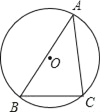
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=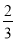 ,求BC的长.
,求BC的长.