题目内容
 如图,点P为正方形ABCD内一点,且PA=1,PB=2,PC=3.试求∠APB的度数.
如图,点P为正方形ABCD内一点,且PA=1,PB=2,PC=3.试求∠APB的度数.分析:将△ABP绕点B顺时针旋转90°,使得AB与BC重合,根据旋转的性质可得△BPP′是等腰直角三角形,然后求出PP′,再根据勾股定理逆定理判定出△PP′C是直角三角形,然后求出∠BP′C的度数,再根据旋转的性质可得∠APB=∠BP′C.
解答: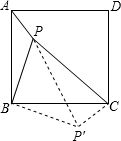 证明:如图,将△ABP绕点B顺时针旋转90°,使得AB与BC重合,
证明:如图,将△ABP绕点B顺时针旋转90°,使得AB与BC重合,
则P′C=PA=1,△BPP′是等腰直角三角形,
∵PB=2,
∴PP′=
PB=2
,
在△PP′C中,PP′2+P′C2=(2
)2+12=9,
PC2=32=9,
∴PP′2+P′C2=PC2,
∴△PP′C是直角三角形,
∠BP′C=∠BP′P+∠PP′C=45°+90°=135°,
∵△CBP′是△ABP绕点B顺时针旋转90°得到,
∴∠APB=∠BP′C=135°.
 证明:如图,将△ABP绕点B顺时针旋转90°,使得AB与BC重合,
证明:如图,将△ABP绕点B顺时针旋转90°,使得AB与BC重合,则P′C=PA=1,△BPP′是等腰直角三角形,
∵PB=2,
∴PP′=
| 2 |
| 2 |
在△PP′C中,PP′2+P′C2=(2
| 2 |
PC2=32=9,
∴PP′2+P′C2=PC2,
∴△PP′C是直角三角形,
∠BP′C=∠BP′P+∠PP′C=45°+90°=135°,
∵△CBP′是△ABP绕点B顺时针旋转90°得到,
∴∠APB=∠BP′C=135°.
点评:本题考查了旋转的性质,主要利用了旋转变换只改变图形的位置不改变图形的形状与大小,勾股定理的逆定理,作出图形并判断出△PP′C是直角三角形是解题的关键.

练习册系列答案
相关题目
 如图,点F为正方形内一点,在正方形外有一点E,满足∠ABF=∠CBE,BF=BE.
如图,点F为正方形内一点,在正方形外有一点E,满足∠ABF=∠CBE,BF=BE.

 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论为( )
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论为( )  如图,点F为正方形ABCD的边CD的中点,E为BC上一点,M为EF上一点,且D、M关于AF对称,B、M关于AE对称,∠CFE的平分线交AE的延长线于G,交BC于N,连CG,下列结论:①△AFG为等腰直角三角形;②CG=2
如图,点F为正方形ABCD的边CD的中点,E为BC上一点,M为EF上一点,且D、M关于AF对称,B、M关于AE对称,∠CFE的平分线交AE的延长线于G,交BC于N,连CG,下列结论:①△AFG为等腰直角三角形;②CG=2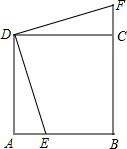 如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.
如图,点E为正方形ABCD的边CD上一点,AB=10,AE=4.△DAE旋转后能与△DCF重合.