题目内容
(2009•漳州)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.(1)判断直线CD和⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,求
 的长.(结果保留π)
的长.(结果保留π)
【答案】分析:(1)连接CO,根据AC=CD,得出∠A=∠D=30°,则∠COD=60°,从而得出∠OCD=90°,则直线CD和⊙O相切;
(2)根据弧长公式l= 进行计算即可.
进行计算即可.
解答: 解:(1)连接CO,∵AC=CD,∴∠A=∠D,
解:(1)连接CO,∵AC=CD,∴∠A=∠D,
∵∠D=30°,∴∠A=30°,
∵OA=OC,∴∠COD=60°,
∴∠OCD=90°,
∴直线CD和⊙O相切;
(2)∵⊙O的半径为3,
∴弧长公式l=
=
=π.
点评:本题考查了切线的判定、弧长的计算,是基础知识要熟练掌握,解题的关键是弧长公式l=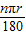 .
.
(2)根据弧长公式l=
 进行计算即可.
进行计算即可.解答:
 解:(1)连接CO,∵AC=CD,∴∠A=∠D,
解:(1)连接CO,∵AC=CD,∴∠A=∠D,∵∠D=30°,∴∠A=30°,
∵OA=OC,∴∠COD=60°,
∴∠OCD=90°,
∴直线CD和⊙O相切;
(2)∵⊙O的半径为3,
∴弧长公式l=

=

=π.
点评:本题考查了切线的判定、弧长的计算,是基础知识要熟练掌握,解题的关键是弧长公式l=
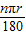 .
. 
练习册系列答案
相关题目



