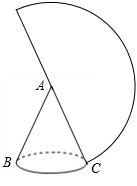
题目内容
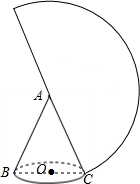 如图,一个圆锥的高为3
如图,一个圆锥的高为3| 3 |
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
分析:(1)直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得比值;
(2)利用圆锥的高,母线和底面半径构造的直角三角形中的勾股定理和等腰三角形的基本性质解题即可;
(3)圆锥的侧面积是展开图扇形的面积,直接利用公式解题即可,圆锥的侧面积为
.
(2)利用圆锥的高,母线和底面半径构造的直角三角形中的勾股定理和等腰三角形的基本性质解题即可;
(3)圆锥的侧面积是展开图扇形的面积,直接利用公式解题即可,圆锥的侧面积为
| πl2 |
| 2 |
解答: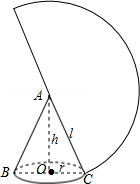 解:
解:
(1)设此圆锥的高为h,底面半径为r,母线长AC=l,
∵2πr=πl,
∴l:r=2:1;
(2)∵AO⊥OC,
=2,
∴圆锥高与母线的夹角为30°,
则∠BAC=60°;
(3)由图可知l2=h2+r2,h=3
cm,
∴(2r)2=(3
)2+r2,即4r2=27+r2,
解得r=3cm,
∴l=2r=6cm,
∴圆锥的侧面积为
=18π(cm2).
 解:
解:(1)设此圆锥的高为h,底面半径为r,母线长AC=l,
∵2πr=πl,
∴l:r=2:1;
(2)∵AO⊥OC,
| l |
| r |
∴圆锥高与母线的夹角为30°,
则∠BAC=60°;
(3)由图可知l2=h2+r2,h=3
| 3 |
∴(2r)2=(3
| 3 |
解得r=3cm,
∴l=2r=6cm,
∴圆锥的侧面积为
| πl2 |
| 2 |
点评:本题主要考查圆锥的特点和圆锥侧面面积的计算.
易错易混点:学生由于空间想象能力不够,找不到圆锥的底面半径,或者对圆锥的侧面面积公式运用不熟练,从而造成错误.
易错易混点:学生由于空间想象能力不够,找不到圆锥的底面半径,或者对圆锥的侧面面积公式运用不熟练,从而造成错误.

练习册系列答案
相关题目
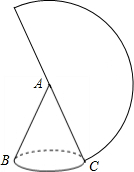 如图,一个圆锥的高为3
如图,一个圆锥的高为3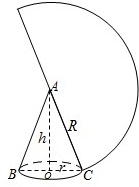 如图,一个圆锥的高为
如图,一个圆锥的高为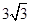 cm,侧面展开图是半圆.
cm,侧面展开图是半圆.