题目内容
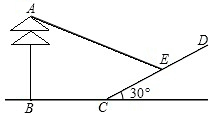 在同一时刻,1m长的标尺的影长为2m,现测得一棵大树AB离山坡CD的距离BC=4m,大树在山坡上的影子长CE=4m,山坡与地平面成30°的角,如图所示,则大树的高度为
在同一时刻,1m长的标尺的影长为2m,现测得一棵大树AB离山坡CD的距离BC=4m,大树在山坡上的影子长CE=4m,山坡与地平面成30°的角,如图所示,则大树的高度为(4+
)
| 3 |
(4+
)
m.| 3 |
分析:延长AE交BC延长线于Q,过E作EF⊥BC于F,根据含30°角的直角三角形性质求出EF=
CE=2,由勾股定理求出CF=2
,根据在同一时刻,1m长的标尺的影长为2m求出EF的影子长FQ,求出AB的影子长,即可求出AB.
| 1 |
| 2 |
| 3 |
解答:解: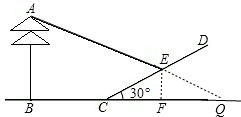 延长AE交BC延长线于Q,过E作EF⊥BC于F,
延长AE交BC延长线于Q,过E作EF⊥BC于F,
则∠EFC=∠EFQ=90°,
∵CE=4,∠ECF=30°,
∴EF=
CE=2,
由勾股定理得:CF=
=2
,
由图可知EF的影子长是FQ,
∵在同一时刻,1m长的标尺的影长为2m,
∴
=
,
∴FQ=4,
即大树的影长为BC+CF+FQ=4+2
+4=8+2
,
∵在同一时刻,1m长的标尺的影长为2m,
∴
=
,
∴AB=4+
(m).
故答案为:(4+
).
 延长AE交BC延长线于Q,过E作EF⊥BC于F,
延长AE交BC延长线于Q,过E作EF⊥BC于F,则∠EFC=∠EFQ=90°,
∵CE=4,∠ECF=30°,
∴EF=
| 1 |
| 2 |
由勾股定理得:CF=
| 42-22 |
| 3 |
由图可知EF的影子长是FQ,
∵在同一时刻,1m长的标尺的影长为2m,
∴
| EF |
| FQ |
| 1 |
| 2 |
∴FQ=4,
即大树的影长为BC+CF+FQ=4+2
| 3 |
| 3 |
∵在同一时刻,1m长的标尺的影长为2m,
∴
| AB | ||
8+2
|
| 1 |
| 2 |
∴AB=4+
| 3 |
故答案为:(4+
| 3 |
点评:本题考查了含30°角的直角三角形性质和解直角三角形的应用,主要考查学生的理解能力和计算能力,用了转化思想,即把实际问题转化成数学问题来解决.

练习册系列答案
相关题目
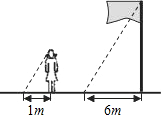 如图,在同一时刻,测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.6m,则旗杆的高约为
如图,在同一时刻,测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.6m,则旗杆的高约为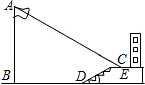 梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据:
梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据: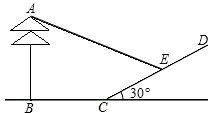 在同一时刻,1m长的标尺的影长为2m,现测得一棵大树AB离山坡CD的距离BC=4m,大树在山坡上的影子长CE=4m,山坡与地平面成30°的角,如图所示,则大树的高度为________ m.
在同一时刻,1m长的标尺的影长为2m,现测得一棵大树AB离山坡CD的距离BC=4m,大树在山坡上的影子长CE=4m,山坡与地平面成30°的角,如图所示,则大树的高度为________ m.