题目内容
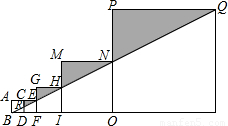
5个正方形如图摆放在同一直线上,线段BQ经过点E、H、N,记△RCE、△GEH、△MHN、△PNQ的面积分别为S1,S2,S3,S4,已知S1+S3=17,则S2+S4= .
【答案】分析:由如图5个正方形摆放在同一直线上,可得tan∠EBF=tan∠AEB=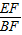 =
= ,∠GHE=∠MNH=∠PQN=∠EBF,然后设DR=a,则EF=BD=CD=CE=2a,根据三角函数的知识,即可得:MH=4a,MN=8a,PN=8a,PQ=16a,又由S1+S3=17,即可求得a2的值,继而可求得S2+S4的值.
,∠GHE=∠MNH=∠PQN=∠EBF,然后设DR=a,则EF=BD=CD=CE=2a,根据三角函数的知识,即可得:MH=4a,MN=8a,PN=8a,PQ=16a,又由S1+S3=17,即可求得a2的值,继而可求得S2+S4的值.
解答:解:∵四边形ABDC与四边形CDFE是正方形,
∴BD=DF=EF,AE∥BF,
∴∠EBF=∠AEB,
∴tan∠EBF=tan∠AEB=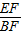 =
= ,
,
同理可得:∠GHE=∠MNH=∠PQN=∠EBF,
设DR=a,则EF=BD=CD=CE=2a,
∴CR=a,
∵tan∠EBF=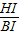 =
= ,
,
∴FI=HI=GH=4a,
∴GE=2a,
同理可得:MH=4a,MN=8a,PN=8a,PQ=16a,
∴S1+S3= ×a×2a+
×a×2a+ ×4a×8a=17,
×4a×8a=17,
解得:a2=1,
∴S2+S4= ×2a×4a+
×2a×4a+ ×8a×16a=68a2=68.
×8a×16a=68a2=68.
故答案为:68.
点评:此题考查了正方形的性质、三角函数的性质以及面积与等积变换问题.此题难度较大,解题的关键是根据题意设DR=a,根据三角函数的知识,求得CE、CR、MH、MN、PN、PQ,然后由S1+S3=17,求得a2的值.
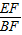 =
= ,∠GHE=∠MNH=∠PQN=∠EBF,然后设DR=a,则EF=BD=CD=CE=2a,根据三角函数的知识,即可得:MH=4a,MN=8a,PN=8a,PQ=16a,又由S1+S3=17,即可求得a2的值,继而可求得S2+S4的值.
,∠GHE=∠MNH=∠PQN=∠EBF,然后设DR=a,则EF=BD=CD=CE=2a,根据三角函数的知识,即可得:MH=4a,MN=8a,PN=8a,PQ=16a,又由S1+S3=17,即可求得a2的值,继而可求得S2+S4的值.解答:解:∵四边形ABDC与四边形CDFE是正方形,
∴BD=DF=EF,AE∥BF,
∴∠EBF=∠AEB,
∴tan∠EBF=tan∠AEB=
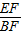 =
= ,
,同理可得:∠GHE=∠MNH=∠PQN=∠EBF,
设DR=a,则EF=BD=CD=CE=2a,
∴CR=a,
∵tan∠EBF=
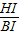 =
= ,
,∴FI=HI=GH=4a,
∴GE=2a,
同理可得:MH=4a,MN=8a,PN=8a,PQ=16a,
∴S1+S3=
 ×a×2a+
×a×2a+ ×4a×8a=17,
×4a×8a=17,解得:a2=1,
∴S2+S4=
 ×2a×4a+
×2a×4a+ ×8a×16a=68a2=68.
×8a×16a=68a2=68.故答案为:68.
点评:此题考查了正方形的性质、三角函数的性质以及面积与等积变换问题.此题难度较大,解题的关键是根据题意设DR=a,根据三角函数的知识,求得CE、CR、MH、MN、PN、PQ,然后由S1+S3=17,求得a2的值.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
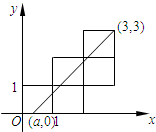 五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是( )
五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
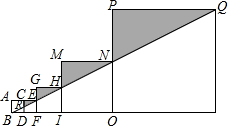 5个正方形如图摆放在同一直线上,线段BQ经过点E、H、N,记△RCE、△GEH、△MHN、△PNQ的面积分别为S1,S2,S3,S4,已知S1+S3=17,则S2+S4=
5个正方形如图摆放在同一直线上,线段BQ经过点E、H、N,记△RCE、△GEH、△MHN、△PNQ的面积分别为S1,S2,S3,S4,已知S1+S3=17,则S2+S4=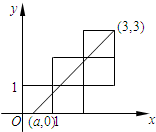 五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是
五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是