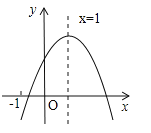��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���֪������![]() ��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
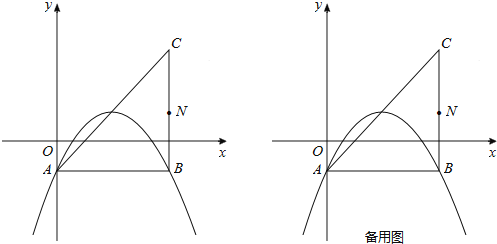
��1����ͼ�����������߹�A��B���㣬��������ߵĺ�������ʽ��
��2��ƽ�ƣ�1���е������ߣ�ʹ����P��ֱ��AC�ϻ���������AC������һ��Q��
��i������M��ֱ��AC�·�����Ϊƽ��ǰ��1���е��������ϵĵ㣬����M��P��Q����Ϊ������������ǵ���ֱ��������ʱ��������з��������ĵ�M�����ꣻ
��ii��ȡBC���е�N������NP��BQ����̽��![]() �Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2����i��M1��4����1����M2����2����7����M3��
����2����i��M1��4����1����M2����2����7����M3��![]() ��
��![]() ����M4��
����M4��![]() ��
��![]() ������ii��
������ii��![]() ��
��
��������
�����������1���������B�����꣬Ȼ�����ô���ϵ������������ߵĺ�������ʽ��
��2����i���������ֱ��AC�Ľ���ʽ���߶�PQ�ij��ȣ���Ϊ��������Ļ�����
����MPQΪ����ֱ�������Σ���ɷ�Ϊ�������������
�ٵ�PQΪֱ�DZ�ʱ����M��PQ�ľ���Ϊ![]() ����ʱ����ֱ��AC����ƽ��4����λ������ֱ�ߣ�y=x��5���������ߵĽ��㣬��Ϊ����֮M�㣻
����ʱ����ֱ��AC����ƽ��4����λ������ֱ�ߣ�y=x��5���������ߵĽ��㣬��Ϊ����֮M�㣻
�ڵ�PQΪб��ʱ����M��PQ�ľ���Ϊ![]() ����ʱ����ֱ��AC����ƽ��2����λ������ֱ�ߣ�y=x��3���������ߵĽ��㣬��Ϊ����֮M�㣮
����ʱ����ֱ��AC����ƽ��2����λ������ֱ�ߣ�y=x��3���������ߵĽ��㣬��Ϊ����֮M�㣮
��ii���ɣ�i����֪��PQ=![]() Ϊ��ֵ����˵�NP+BQȡ��Сֵʱ��
Ϊ��ֵ����˵�NP+BQȡ��Сֵʱ��![]() �����ֵ��
�����ֵ��
���ͼ2��ʾ������B����ֱ��AC�ĶԳƵ�B�䣬�ɷ�����֪����B�䡢Q��F��AB�е㣩���㹲��ʱ��NP+BQ��С����СֵΪ�߶�B��F�ij��ȣ�
�����������1��������ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3��
����B��������4����1����
�������߹�A��0����1����B��4����1�����㣬�� ����ã�b=2��c=��1���������ߵĺ�������ʽΪ��
����ã�b=2��c=��1���������ߵĺ�������ʽΪ��![]() ��
��
��2����i��
��A��0��1����C��4��3������lAC��y=x��1���������߶���P��ֱ��AC�ϣ���P��t��t��1�����������߱���ʽ��![]() ����lAC�������ߵĽ���Q��t��2��t��3������һM��P��Q����Ϊ������������ǵ���ֱ�������Σ�P��t��t��1����
����lAC�������ߵĽ���Q��t��2��t��3������һM��P��Q����Ϊ������������ǵ���ֱ�������Σ�P��t��t��1����
�ٵ�MΪֱ�Ƕ���ʱ��M��t��t��3����![]() ����t=
����t=![]() ����M1��
����M1��![]() ��
��![]() ����M2��
����M2��![]() ��
��![]() ����
����
�ڵ�QΪֱ�Ƕ���ʱ����M����Ϊ��P�Ƶ�Q˳ʱ����ת90����ɣ�����Q��t��2��t��3��ƽ����ԭ��Q�䣨0��0�������Pƽ�ƺ�P�䣨2��2��������P����ԭ��˳ʱ����ת90�㣬���M�䣨2����2������Q�䣨0��0��ƽ������Q��t��2��t��3�������M��ƽ�ƺ�Ϊ��M��t��t��5������![]() ����t1=4��t2=��2����M1��4����1����M2����2����7����
����t1=4��t2=��2����M1��4����1����M2����2����7����
�۵�PΪֱ�Ƕ���ʱ��ͬ���ɵ�M1��4����1����M2����2����7�����������������з��������ĵ�M������Ϊ��
M1��4����1����M2����2����7����M3��![]() ��
��![]() ����M4��
����M4��![]() ��
��![]() ����
����
��ii��![]() �������ֵ���������£�
�������ֵ���������£�
����i��֪PQ=![]() Ϊ��ֵ����NP+BQȡ��Сֵʱ��
Ϊ��ֵ����NP+BQȡ��Сֵʱ��![]() �����ֵ��
�����ֵ��
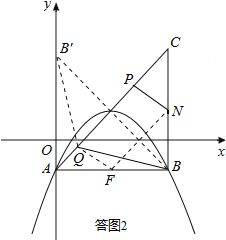
���ͼ2��ȡ��B����AC�ĶԳƵ�B�䣬�õ�B�������Ϊ��0��3����BQ=B��Q��
����QF��FN��QB�䣬��FN��PQ����FN=PQ�����ı���PQFNΪƽ���ı��Σ���NP=FQ����NP+BQ=FQ+B��Q��FB��=![]() =
=![]() ������B�䡢Q��F���㹲��ʱ��NP+BQ��С����СֵΪ
������B�䡢Q��F���㹲��ʱ��NP+BQ��С����СֵΪ![]() ����
����![]() �����ֵΪ
�����ֵΪ![]() =
=![]() ��
��