Question

【题目】在由6个大小相同的小正方形组成的方格中：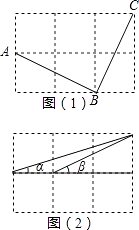

（1）如图（1），A、B、C是三个格点（即小正方形的顶点），判断AB与BC的关系，并说明理由；
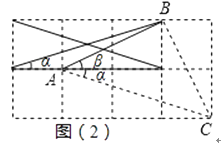
（2）如图（2），连结三格和两格的对角线，求∠α+∠β的度数（要求：画出示意图并给出证明）．

Answer 1

【答案】
（1）

解：如图，连接AC，

由勾股定理得，AB2=12+22=5，

BC2=12+22=5，

AC2=12+32=10，

∴AB2+BC2=AC2，

∴△ABC是直角三角形，∠ABC=90°，

∴AB⊥BC

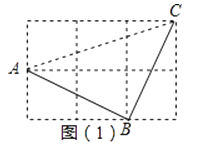
（2）

解：∠α+∠β=45°．

证明如下：如图，由勾股定理得，AB2=12+22=5，

BC2=12+22=5，

AC2=12+32=10，

∴AB2+BC2=AC2，

∴△ABC是直角三角形，

∵AB=BC，

∴△ABC是等腰直角三角形，

∴∠α+∠β=45°．

【解析】（1）连接AC，再利用勾股定理列式求出AB2、BC2、AC2 ， 然后利用勾股定理逆定理解答；（2）类似于（1）的图形解答．
【考点精析】根据题目的已知条件，利用勾股定理的概念和勾股定理的逆定理的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．