题目内容
(2002•泉州)要使函数y=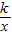 (k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k的值可取为 (请你写出能符合上述要求的两个数值).
(k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k的值可取为 (请你写出能符合上述要求的两个数值).
【答案】分析:因为函数y=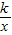 (k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k应取>0的数,则能符合上述要求的两个数值可以是1,2(或其他正数).
(k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k应取>0的数,则能符合上述要求的两个数值可以是1,2(或其他正数).
解答:解:∵函数图象在一三象限,
∴k>0,
那么1,2符合条件.
点评:此题主要考查反比例函数图象的性质:(1)k>0时,图象是位于一、三象限;(2)k<0时,图象是位于二、四象限.
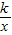 (k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k应取>0的数,则能符合上述要求的两个数值可以是1,2(或其他正数).
(k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k应取>0的数,则能符合上述要求的两个数值可以是1,2(或其他正数).解答:解:∵函数图象在一三象限,
∴k>0,
那么1,2符合条件.
点评:此题主要考查反比例函数图象的性质:(1)k>0时,图象是位于一、三象限;(2)k<0时,图象是位于二、四象限.

练习册系列答案
相关题目
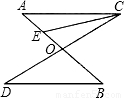
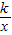 (k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k的值可取为 (请你写出能符合上述要求的两个数值).
(k是常数,k≠0)的图象的两个分支分别在第一、三象限内,则k的值可取为 (请你写出能符合上述要求的两个数值).