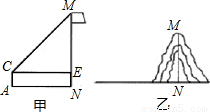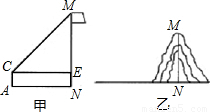题目内容
同学们在学完解直角三角形的应用后,某合作学习小组用测倾器、皮尺测量了学校旗杆的高度,他们设计了如下方案(如图所示):①在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=30°;
②量出测点A到旗杆底部N的水平距离AN=20m;
③量出测倾器的高度AC=1m.
(1)根据上述测量数据,即可求出旗杆的高度MN=
(2)如果测量工具不变,请仿照上述过程,设计一个测量某小山高度(如图)的方案.要求:
(ⅰ)在图中,画出你测量小山高度MN的示意图(标上适当字母);
(ⅱ)写出你设计的方案.(测倾器的高度用h表示,其它涉及的长度用字母a、b、c…表示,涉
 及到的角度用α、β…表示,最后请给出计算MN的高度的式子).
及到的角度用α、β…表示,最后请给出计算MN的高度的式子).
分析:(1)在RT△MCE中,知道30°角的邻边求对边,直接用正切值计算即可;
(2)构建两个直角三角形,利用仰角的正切进行解答.
(2)构建两个直角三角形,利用仰角的正切进行解答.
解答: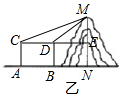 解:(1)在RT△MCE中,ME=CEtan30°=20×
解:(1)在RT△MCE中,ME=CEtan30°=20×
,
又因为EN=AC=1,所以MN=1+
;
(2)
①在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
②向前移动至点B,量出测点A到点B的水平距离AB=a;
③在测点B处安置测倾器,测得旗杆顶部M的仰角∠MDE=β;
④量出测倾器的高度AC=h.
∵设ME=x,
∴CE=
,DE=
,
∴CD=CE-DE=
-
=a,
∴ME=
,
根据上述测量数据,即可求出小山的高度:MN=h+
.
 解:(1)在RT△MCE中,ME=CEtan30°=20×
解:(1)在RT△MCE中,ME=CEtan30°=20×
| ||
| 3 |
又因为EN=AC=1,所以MN=1+
20
| ||
| 3 |
(2)
①在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
②向前移动至点B,量出测点A到点B的水平距离AB=a;
③在测点B处安置测倾器,测得旗杆顶部M的仰角∠MDE=β;
④量出测倾器的高度AC=h.
∵设ME=x,
∴CE=
| ME |
| tanα |
| ME |
| tanβ |
∴CD=CE-DE=
| ME |
| tanα |
| ME |
| tanβ |
∴ME=
| a•tanα•tanβ |
| tanβ-tanα |
根据上述测量数据,即可求出小山的高度:MN=h+
| a•tanα•tanβ |
| tanβ-tanα |
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 及到的角度用α、β…表示,最后请给出计算MN的高度的式子).
及到的角度用α、β…表示,最后请给出计算MN的高度的式子).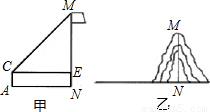 及到的角度用α、β…表示,最后请给出计算MN的高度的式子).
及到的角度用α、β…表示,最后请给出计算MN的高度的式子).