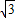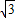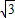题目内容
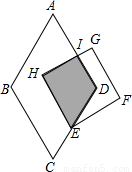
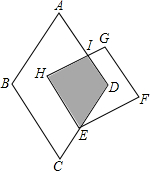 如图为菱形ABCD与正方形EFGH的重叠情形,其中E在CD上,AD与GH相交于I点,且AD∥HE.若∠A=60°,且AB=7,DE=4,HE=5,则梯形HEDI的面积为
如图为菱形ABCD与正方形EFGH的重叠情形,其中E在CD上,AD与GH相交于I点,且AD∥HE.若∠A=60°,且AB=7,DE=4,HE=5,则梯形HEDI的面积为8
| 3 |
8
.| 3 |
分析:利用菱形和正方形的性质分别求得HE和ID、DE的长,利用梯形的面积计算方法算得梯形的面积即可.
解答: 解:∵四边形ABCD为菱形且∠A=60°,
解:∵四边形ABCD为菱形且∠A=60°,
∴∠ADE=180°-60°=120°,
又∵AD∥HE
∴∠DEH=180°-120°=60°,
作DM⊥HE于M点,则△DEM为30°-60°-90°的三角形,
又∵DE=4
∴EM=2,DM=2
,
且四边形EFGH为正方形
∴∠H=∠DIH=90°,
即四边形IDMH为矩形,
∴ID=HM=5-2=3,
∴梯形HEDI面积=
=8
.
故答案为:8
.
 解:∵四边形ABCD为菱形且∠A=60°,
解:∵四边形ABCD为菱形且∠A=60°,∴∠ADE=180°-60°=120°,
又∵AD∥HE
∴∠DEH=180°-120°=60°,
作DM⊥HE于M点,则△DEM为30°-60°-90°的三角形,
又∵DE=4
∴EM=2,DM=2
| 3 |
且四边形EFGH为正方形
∴∠H=∠DIH=90°,
即四边形IDMH为矩形,
∴ID=HM=5-2=3,
∴梯形HEDI面积=
(3+5)×2
| ||
| 2 |
| 3 |
故答案为:8
| 3 |
点评:本题考查了梯形的面积的计算,解题的关键是正确地利用菱形和正方形的性质计算梯形的底和高.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
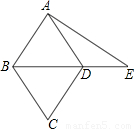
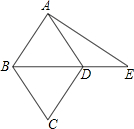 如图为菱形ABCD与△ABE的重迭情形,其中D在BE上.若AB=17,BD=16,AE=25,则DE的长度为何?( )
如图为菱形ABCD与△ABE的重迭情形,其中D在BE上.若AB=17,BD=16,AE=25,则DE的长度为何?( )| A、8 | B、9 | C、11 | D、12 |
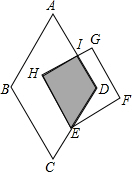 如图为菱形ABCD与正方形EFGH的重迭情形,其中E在CD上,AD与GH相交于I点,且AD∥HE.若∠A=60°,且AB=7,DE=4,HE=5,则梯形HEDI的面积为何?( )
如图为菱形ABCD与正方形EFGH的重迭情形,其中E在CD上,AD与GH相交于I点,且AD∥HE.若∠A=60°,且AB=7,DE=4,HE=5,则梯形HEDI的面积为何?( )A、6
| ||
B、8
| ||
C、10-2
| ||
D、10+2
|