题目内容
△ABC和△DBE是绕点B旋转的两个相似三角形,其中∠ABC与∠DBE、∠A与∠D为对应角.
(1)如图1,若△ABC和△DBE分别是以∠ABC与∠DBE为顶角的等腰直角三角形,且两三角形旋转到使点B、C、D在同一条直线上的位置时,请直接写出线段AD与线段EC的关系;
(2)若△ABC和△DBE为含有30°角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段AD与线段EC的关系,并说明理由;
(3)若△ABC和△DBE为如图3的两个三角形,且∠ACB=α,∠BDE=β,在绕点B旋转的过程中,直线AD与EC夹角的度数是否改变?若不改变,直接用含α、β的式子表示夹角的度数;若改变,请说明理由.

解:(1)线段AD与线段CE的关系是AD⊥EC,AD=EC;
理由:连接AD、CE;
∵△ABC、△BED都是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠EBD=90°,
∴△ABD≌△CBE,
∴AD=CE,∠DAB=∠BCE;
∵∠BEC+∠BCE=90°,
∴∠BEC+∠DAE=90°,即AD⊥CE;
故线段AD与线段EC的关系是AD⊥EC,AD=EC.
(2)如图2,连接AD、EC并延长,设交点为点F;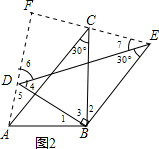
∵△ABC∽△DBE,
∴ ,
,
∴ .
.
∵∠ABC=∠DBE=90°,
∴∠1+∠3=90°,∠2+∠3=90°
∴∠1=∠2
∴△ABD∽△CBE.
∴ .
.
在Rt△ACB中, ,∵
,∵ ,
,
∴ .
.
又∵∠DBE=90°,∠DEB=30°,
∴∠4=60°,
∴∠5+∠6=120°.
∵△ABD∽△CBE,
∴∠5=∠CEB=30°+∠7,
∴∠7=∠5-30°,∠6=120°-∠5,
∴∠7+∠6=90°,
∴∠DFE=90°
即AD⊥CE.
(3)在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,且∠AFE=(180-α-β)度.
分析:(1)连接AD、CE,然后证得△ABD≌△BCE,根据所得的等角和等边来判断AD、EC的关系.
(2)连接AD、EC并延长,设交点为点F,根据已知条件,易证得△ABD∽△CBE,得AB:BC=BD:BE,而∠1、∠2同为∠3的余角,则可证得△ABD=△CBE,得∠5=∠7+30°,而∠6=120°-∠5,由此可证得∠7+∠6=90°,即AD⊥CE.
(3)根据上面的求解过程可知:在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,解题思路和方法同(2).
点评:本题考查了图形的旋转变化以及相似三角形的判定和性质,理清图中角与角之间的关系,是解答此题的关键.

理由:连接AD、CE;
∵△ABC、△BED都是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠EBD=90°,
∴△ABD≌△CBE,
∴AD=CE,∠DAB=∠BCE;
∵∠BEC+∠BCE=90°,
∴∠BEC+∠DAE=90°,即AD⊥CE;
故线段AD与线段EC的关系是AD⊥EC,AD=EC.
(2)如图2,连接AD、EC并延长,设交点为点F;

∵△ABC∽△DBE,
∴
 ,
,∴
 .
.∵∠ABC=∠DBE=90°,
∴∠1+∠3=90°,∠2+∠3=90°
∴∠1=∠2
∴△ABD∽△CBE.
∴
 .
.在Rt△ACB中,
 ,∵
,∵ ,
,∴
 .
.又∵∠DBE=90°,∠DEB=30°,
∴∠4=60°,
∴∠5+∠6=120°.
∵△ABD∽△CBE,
∴∠5=∠CEB=30°+∠7,
∴∠7=∠5-30°,∠6=120°-∠5,
∴∠7+∠6=90°,
∴∠DFE=90°
即AD⊥CE.
(3)在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,且∠AFE=(180-α-β)度.
分析:(1)连接AD、CE,然后证得△ABD≌△BCE,根据所得的等角和等边来判断AD、EC的关系.
(2)连接AD、EC并延长,设交点为点F,根据已知条件,易证得△ABD∽△CBE,得AB:BC=BD:BE,而∠1、∠2同为∠3的余角,则可证得△ABD=△CBE,得∠5=∠7+30°,而∠6=120°-∠5,由此可证得∠7+∠6=90°,即AD⊥CE.
(3)根据上面的求解过程可知:在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,解题思路和方法同(2).
点评:本题考查了图形的旋转变化以及相似三角形的判定和性质,理清图中角与角之间的关系,是解答此题的关键.

练习册系列答案
相关题目


 ,∠BDE=
,∠BDE= ,在绕点B旋转的过程中,直线AD与EC夹角的度数是否改变?若不改变,直接用含
,在绕点B旋转的过程中,直线AD与EC夹角的度数是否改变?若不改变,直接用含 、
、 的式子表示夹角的度数;若改变,请说明理由。
的式子表示夹角的度数;若改变,请说明理由。
