题目内容
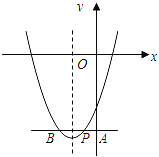
【题目】如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，当P运动到B点时，P、Q两点同时停止运动．设P点运动的时间为t秒，△APQ的面积为S，则表示S与t之间的函数关系的图象大致是（ ）
A．
B．
C．
D．
【答案】D
【解析】
试题分析：根据动点P从A点出发，到B停止，速度为每秒1个单位，则时间为0～4秒，动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，路程为8，时间为0～4秒； 分两种情况：
①当0＜t≤2时，如图1，Q在BC上，则△APQ的面积为S=
APBQ=t2，图象为二次函数的抛物线； 由题意得：AP=t，BQ=2t S△APQ=
APBQ=t2t=t2，其图象是抛物线，
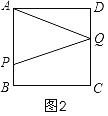
②当2＜t≤4时，如图2，点Q在CD上，其面积求得为2t，是一条直线；作出判断． S△APQ=APBC=×t×4=2t，其图象为一条直线
练习册系列答案
轻松暑假总复习系列答案
相关题目
