题目内容
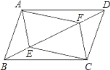
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,将矩形沿
,将矩形沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,则折痕
重合,则折痕![]() 的长为( )
的长为( )
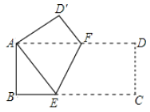
A.6B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据折叠的性质得到EF垂直平分AC,即OA=OC,FA=FC,∠AOF=90°,设AF=x,则FC=x,BF=BC-x=10-x,在Rt△ABF中根据勾股定理列方程可计算出x,在Rt△ABC中根据勾股定理可计算出AC,可得OA的长,在Rt△AOF中利用勾股定理可计算出OF;易证得△AOE≌△COF,得到OE=OF,则EF=2OF.
解:连结AC,如图,
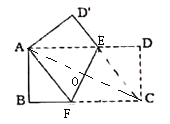
∵矩形折叠后点C与点A重合,
∴EF垂直平分AC,即OA=OC,FA=FC,∠AOF=90°,
设AF=x,则FC=x,BF=BC-x=10-x,
在Rt△ABF中,AB2+BF2=AF2,即52+(10-x)2=x2,解得x=![]() ,
,
在Rt△ABC中,AC=![]() =
=![]() ,
,
∴OA=![]() ,
,
在Rt△AOF中,OF=![]() =
=![]() ,
,
∵AD∥BC,
∴∠DAC=∠BCA,
∵在△AOE和△COF中, ,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴EF=2OF=![]() .
.
故选:D.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目