题目内容
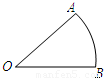
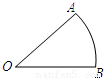
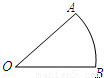
（2010•大庆）如图，已知∠AOB=30°，M为OB边上一点，以M为圆心、2cm为半径作M．若⊙M在OB边上运动，则当OM= cm时，⊙M与OA相切．
【答案】分析：连接MN，N为切点，根据MN⊥AO可知∠AOB=30°，2cm为半径，利用直角三角形中30°的角所对的直角边是斜边的一半解答．
解答：
解：连接MN，
∵MN⊥AO，∠AOB=30°，2cm为半径，
∴OM=2MN=2×2=4cm．
故当OM=4cm时，⊙M与OA相切．
点评：根据直角三角形中，30°的角所对的直角边是斜边的一半解答．
解答：
解：连接MN，∵MN⊥AO，∠AOB=30°，2cm为半径，
∴OM=2MN=2×2=4cm．
故当OM=4cm时，⊙M与OA相切．
点评：根据直角三角形中，30°的角所对的直角边是斜边的一半解答．
练习册系列答案
相关题目
