题目内容
小红和小明在操场做游戏,他们分别在地上画了周长为4米的圆和正方形(如图1),蒙上眼在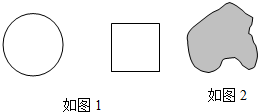 一定距离外向圆和正方形内掷小石子,谁投进的次数多谁就胜.
一定距离外向圆和正方形内掷小石子,谁投进的次数多谁就胜.(1)你认为游戏公平吗?为什么?
(2)如图2是一块不规则形状的图形,你能否用频率估计概率的方法,来估算这个非规则图形的面积呢?请你设计方案,解决这一问题.(要求画出图形,说明设计步骤、原理,写出公式)
分析:(1)根据圆的周长即可得出半径,再利用正方形的周长的得出边长分别求出即可;
(2)根据实验或面积求法分别分析即可得出答案.
(2)根据实验或面积求法分别分析即可得出答案.
解答:解:(1)C圆=4,
∴2πr=4r=
S⊙O=πr2=π(
)2=
=1.273(1分)
C正方形=4,
∴a=1,
∴S正方形=1(2分),
∵S圆>S正(3分),
抛入圆内的可能性大于投入正方形内的可能性,所以不公平(4分).
(2)能.(5分)
①用可测量的规则图形正方形,设其面积为S,将非规则图形围起来.
②往图形中掷点,(如蒙上眼睛掷石子,掷在形外不作记录)
③当掷点数充分大(如1万次),记录并统计结果,掷入正方形内m次,其中n次掷入非规则图形内(6分)
④设非规则图形面积为S′,用频率估计概率,
即频率P′(掷入非规则图形内)=
≈概率P(掷入非规则图形内)=
,
故
=
(7分),
∴S′=
S(8分).
∴2πr=4r=
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
C正方形=4,
∴a=1,
∴S正方形=1(2分),
∵S圆>S正(3分),
抛入圆内的可能性大于投入正方形内的可能性,所以不公平(4分).
(2)能.(5分)
①用可测量的规则图形正方形,设其面积为S,将非规则图形围起来.
②往图形中掷点,(如蒙上眼睛掷石子,掷在形外不作记录)
③当掷点数充分大(如1万次),记录并统计结果,掷入正方形内m次,其中n次掷入非规则图形内(6分)
④设非规则图形面积为S′,用频率估计概率,
即频率P′(掷入非规则图形内)=
| n |
| m |
| S′ |
| S |
故
| n |
| m |
| S′ |
| S |
∴S′=
| n |
| m |
点评:此题主要考查了圆的周长公式以及利用频率求概率,熟练应用圆的周长公式以及利用频率估计概率是解决问题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

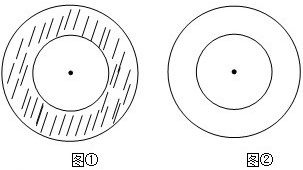 (2008•荔湾区二模)小红和小明在操场做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如图①),蒙上眼在一定距离外向圈内掷小石子.掷中阴影小红胜,否则小明胜,未掷入圈内或掷中两圆的边界线则重掷.
(2008•荔湾区二模)小红和小明在操场做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如图①),蒙上眼在一定距离外向圈内掷小石子.掷中阴影小红胜,否则小明胜,未掷入圈内或掷中两圆的边界线则重掷.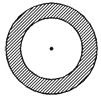 小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.