题目内容
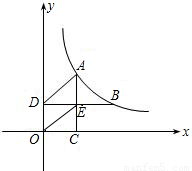
如图,A,B为双曲线y= (k>0)上两点,AC⊥x轴于C,BD⊥y轴于D交AC于E,若矩形OCED面积为2且AD∥OE,则k= .
(k>0)上两点,AC⊥x轴于C,BD⊥y轴于D交AC于E,若矩形OCED面积为2且AD∥OE,则k= .
【答案】分析:根据题意:有S矩形OCED=S△OAC;根据反比例函数 中k的几何意义,图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|,列出方程,进而求出k的值.
|k|,列出方程,进而求出k的值.
解答:解:∵AD∥OE,AE∥OD,
∴四边形ADOE是平行四边形,
∴OD=AE,
又易证OD=CE,
∴AE=CE,
∴AC=2CE,
∴S矩形OCED=S△OAC,
∴S= |k|=2,
|k|=2,
又k>0,
∴k=4.
故答案为:4.
点评:主要考查了反比例函数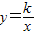 中k的几何意义和几何性质结合的综合应用,有一定的难度.
中k的几何意义和几何性质结合的综合应用,有一定的难度.
 中k的几何意义,图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义,图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|,列出方程,进而求出k的值.
|k|,列出方程,进而求出k的值.解答:解:∵AD∥OE,AE∥OD,
∴四边形ADOE是平行四边形,
∴OD=AE,
又易证OD=CE,
∴AE=CE,
∴AC=2CE,
∴S矩形OCED=S△OAC,
∴S=
 |k|=2,
|k|=2,又k>0,
∴k=4.
故答案为:4.
点评:主要考查了反比例函数
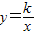 中k的几何意义和几何性质结合的综合应用,有一定的难度.
中k的几何意义和几何性质结合的综合应用,有一定的难度. 
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
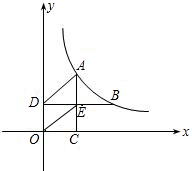 如图,A,B为双曲线y=
如图,A,B为双曲线y=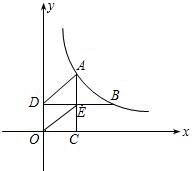
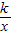 (k>0)上两点,AC⊥x轴于C,BD⊥y轴于D交AC于E,若矩形OCED面积为2且AD∥OE,则k= .
(k>0)上两点,AC⊥x轴于C,BD⊥y轴于D交AC于E,若矩形OCED面积为2且AD∥OE,则k= .
 (k>0)上两点,AC⊥x轴于C,BD⊥y轴于D交AC于E,若矩形OCED面积为2且AD∥OE,则k= .
(k>0)上两点,AC⊥x轴于C,BD⊥y轴于D交AC于E,若矩形OCED面积为2且AD∥OE,则k= .