题目内容
如图,直线AB、CD相交与点O,OE⊥AB与点O,且∠COE=40º,则∠BOD为 .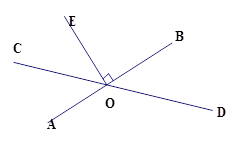

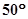
本题考查了垂线、对顶角、邻补角的相关知识。
分析:根据垂直的定义求得∠AOE=90°;然后根据余角的定义可以推知∠AOC=∠AOE-∠COE=50°;最后由对顶角的性质可以求得∠BOD=∠AOC=50°。
解答:
解:∵OE⊥AB,
∴∠AOE=90°;
又∵∠COE=40°,
∴∠AOC=∠AOE-∠COE=50°,
∴∠BOD=∠AOC=50°(对顶角相等);
故∠BOD为50°。

练习册系列答案
相关题目

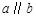 ,则
,则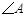 的度数是( ).
的度数是( ).