题目内容
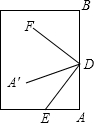 如图所示:文文把一张长方形的纸片折叠了两次,使A、B两点都落在DA′上,折痕分别是DE、DF,则∠EDF的度数为( )
如图所示:文文把一张长方形的纸片折叠了两次,使A、B两点都落在DA′上,折痕分别是DE、DF,则∠EDF的度数为( )分析:根据折叠的性质得∠A′DF=∠BDF,∠A′DE=∠ADE,然后根据平角的定义得到∠A′DF+∠A′DE=
(∠A′DB+∠A′DA)=
×180°=90°.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵长方形的纸片折叠了两次,使A、B两点都落在DA′上,折痕分别是DE、DF,
∴∠A′DF=∠BDF,∠A′DE=∠ADE,
∴∠A′DF+∠A′DE=
(∠A′DB+∠A′DA)=
×180°=90°,
即∠EDF=90°.
故选C.
∴∠A′DF=∠BDF,∠A′DE=∠ADE,
∴∠A′DF+∠A′DE=
| 1 |
| 2 |
| 1 |
| 2 |
即∠EDF=90°.
故选C.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了平角的定义.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
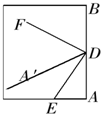 6、如图所示,文文把一张长方形的纸沿着DE、DF折了两次,使A、B都落在DA′上,则∠EDF的度数为( )
6、如图所示,文文把一张长方形的纸沿着DE、DF折了两次,使A、B都落在DA′上,则∠EDF的度数为( )
 A.60° B.75° C.90° D.120°
A.60° B.75° C.90° D.120°