题目内容
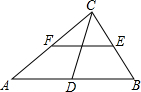（2013•郑州模拟）如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，则EF=5
5
cm．分析：首先根据在直角三角形中，斜边上的中线等于斜边的一半可得AB=2CD=10cm，再根据中位线的性质可得EF=
AB=5cm．
| 1 |
| 2 |
解答：解：∵∠ACB=90°，D为AB中点，
∴AB=2CD，
∵CD=5cm，
∴AB=10cm，
∵E、F分别是BC、CA的中点，
∴EF=
AB=5cm，
故答案为：5．
∴AB=2CD，
∵CD=5cm，
∴AB=10cm，
∵E、F分别是BC、CA的中点，
∴EF=
| 1 |
| 2 |
故答案为：5．
点评：此题主要考查了三角形中位线的性质以及直角三角形的性质，关键是掌握在直角三角形中，斜边上的中线等于斜边的一半．三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
相关题目
（2013•郑州模拟）已知：如图，CF平分∠DCE，点C在BD上，CE∥AB．若∠ECF=55°，则∠ABD的度数为（ ）