题目内容
计算：的结果为__________
已知函数y=，则自变量x的取值范围是（ ）
A. ﹣1＜x＜1 B. x≥﹣1且x≠1 C. x≥﹣1 D. x≠1
观察下面由正整数组成的数阵：
照此规律，按从上到下、从左到右的顺序，第18行的第18个数是_____．
已知抛物线y＝a（x2－cx－2c2）（a＞0）交x轴于A、B两点（点A在点B的左侧），交y轴于点C．
（1） 取A（－1，0），则点B的坐标为___________；
（2） 若A（－1，0），a＝1，点P为第一象限的抛物线，以P为圆心，为半径的圆恰好与AC相切，求P点坐标；
（3） 如图，点R（0，n）在y轴负半轴上，直线RB交抛物线于另一点D，直线RA交抛物线于E．若DR＝DB，EF⊥y轴于F，求的值．
解方程：5x－1＝3(x－1)
如图，为估算学校的旗杆的高度，身高米的小红同学沿着旗杆在地面的影子由向走去，当她走到点处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得，，则旗杆的高度是（ ）
A. 6.4m B. 7m C. 8m D. 9m
将△ABC的边AB绕点A顺时针旋转α得到AB′，边AC绕点A逆时针旋转β得到AC′，α＋β=180°．连接B′C′，作△AB′C′的中线AD．
（初步感知）
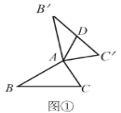
（1）如图①，当∠BAC=90°，BC＝4时，AD的长为______；
（探索证明）
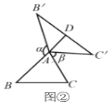
（2）如图②，△ABC为任意三角形时，猜想AD与BC的数量关系，并证明；
（应用延伸）
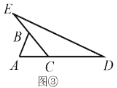
（3）如图③，已知等腰△ACB，AC=BC=m，延长AC到D，延长CB到E，使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′，连接BE′、AD′，若∠CBE′=90°，求AD′的长度（用含m、n的代数式表示）．
方程x2=2x的根是_________.
如图，在3×3的正方形网格中，每个小正方形的边长均为1，△ABC的顶点均在格点上．分别在图①、图②中完成下列画图．要求：仅用无刻度的直尺，且保留必要的画图痕迹．
（1）在图①中的线段AB上找到一点M，作直线CM，使直线CM将△ABC的面积平分．
（2）在图②中的线段AB上找到一点N，作直线CN，使直线CN将△ABC的面积分成1:2的两部分．
的结果为__________
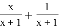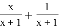阅读快车系列答案阅读快车系列答案的结果为__________阅读快车系列答案
，则自变量x的取值范围是（ ）
为半径的圆恰好与AC相切，求P点坐标；
的值．
2x的根是_________.
