题目内容
(2013•北京)在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图1,直接写出∠ABD的大小(用含α的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.
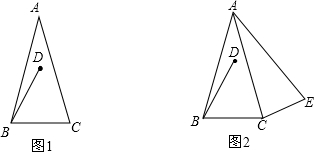
(1)如图1,直接写出∠ABD的大小(用含α的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.
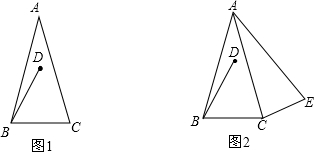
分析:(1)求出∠ABC的度数,即可求出答案;
(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°-
α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=
∠BAC=
α,求出∠BEC=
α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;
(3)求出∠DCE=90°,△DEC为等腰直角三角形,推出DC=CE=BC,求出∠EBC=15°,得出方程30°-
α=15°,求出即可.
(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)求出∠DCE=90°,△DEC为等腰直角三角形,推出DC=CE=BC,求出∠EBC=15°,得出方程30°-
| 1 |
| 2 |
解答: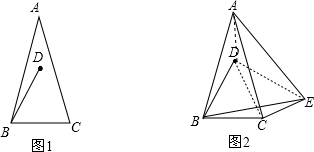 解:(1)∵AB=AC,∠A=α,
解:(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=
(180°-∠A)=90°-
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
即∠ABD=30°-
α;
(2)△ABE是等边三角形,
证明:连接AD,CD,ED,
∵线段BC绕B逆时针旋转60°得到线段BD,
则BC=BD,∠DBC=60°,
∵∠ABE=60°,
∴∠ABD=60°-∠DBE=∠EBC=30°-
α,且△BCD为等边三角形,
在△ABD与△ACD中
∴△ABD≌△ACD,
∴∠BAD=∠CAD=
∠BAC=
α,
∵∠BCE=150°,
∴∠BEC=180°-(30°-
α)-150°=
α=∠BAD,
在△ABD和△EBC中
∴△ABD≌△EBC,
∴AB=BE,
∴△ABE是等边三角形;
(3)∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BC,
∵∠BCE=150°,
∴∠EBC=
(180°-150°)=15°,
∵∠EBC=30°-
α=15°,
∴α=30°.
 解:(1)∵AB=AC,∠A=α,
解:(1)∵AB=AC,∠A=α,∴∠ABC=∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
即∠ABD=30°-
| 1 |
| 2 |
(2)△ABE是等边三角形,
证明:连接AD,CD,ED,
∵线段BC绕B逆时针旋转60°得到线段BD,
则BC=BD,∠DBC=60°,
∵∠ABE=60°,
∴∠ABD=60°-∠DBE=∠EBC=30°-
| 1 |
| 2 |
在△ABD与△ACD中
|
∴△ABD≌△ACD,
∴∠BAD=∠CAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BCE=150°,
∴∠BEC=180°-(30°-
| 1 |
| 2 |
| 1 |
| 2 |
在△ABD和△EBC中
|
∴△ABD≌△EBC,
∴AB=BE,
∴△ABE是等边三角形;
(3)∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BC,
∵∠BCE=150°,
∴∠EBC=
| 1 |
| 2 |
∵∠EBC=30°-
| 1 |
| 2 |
∴α=30°.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定,等腰直角三角形的判定和性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 (2013•北京)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(2013•北京)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B. (2013•北京)对于平面直角坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的关联点.已知点D(
(2013•北京)对于平面直角坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的关联点.已知点D(