题目内容
已知y=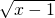 +
+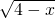 (x,y均为实数),则y的最大值与最小值的差为
(x,y均为实数),则y的最大值与最小值的差为
- A.
 -3
-3 - B.3
- C.
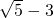
- D.
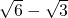
D
分析:先根据二次根式有意义的条件求出x的取值范围,再将y=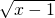 +
+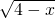 两边同时平方,可得y2=x-1+4-x+2
两边同时平方,可得y2=x-1+4-x+2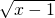
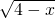 =3+2
=3+2 ,从而可求y的最大值与最小值的差.
,从而可求y的最大值与最小值的差.
解答:根据二次根式有意义,分式有意义得:x-1≥0且4-x≥0,
解得1≤x≤4.
y2=x-1+4-x+2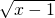
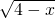 =3+2
=3+2 ,
,
故当x=2.5时,y有最大值 ;
;
当x=1或4时,y有最小值 .
.
∴y的最大值与最小值的差为 -
- .
.
故选D.
点评:本题考查了二次根式的意义和性质.求y的最大值与最小值的差的关键是将y=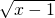 +
+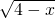 两边同时平方,得出y2=x-1+4-x+2
两边同时平方,得出y2=x-1+4-x+2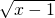
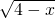 =3+2
=3+2 .
.
分析:先根据二次根式有意义的条件求出x的取值范围,再将y=
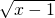 +
+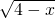 两边同时平方,可得y2=x-1+4-x+2
两边同时平方,可得y2=x-1+4-x+2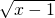
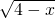 =3+2
=3+2 ,从而可求y的最大值与最小值的差.
,从而可求y的最大值与最小值的差.解答:根据二次根式有意义,分式有意义得:x-1≥0且4-x≥0,
解得1≤x≤4.
y2=x-1+4-x+2
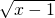
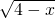 =3+2
=3+2 ,
,故当x=2.5时,y有最大值
 ;
;当x=1或4时,y有最小值
 .
.∴y的最大值与最小值的差为
 -
- .
.故选D.
点评:本题考查了二次根式的意义和性质.求y的最大值与最小值的差的关键是将y=
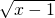 +
+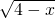 两边同时平方,得出y2=x-1+4-x+2
两边同时平方,得出y2=x-1+4-x+2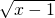
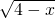 =3+2
=3+2 .
. 
练习册系列答案
相关题目
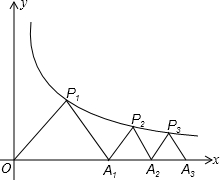 如图,已知△OP1A1、△A1P2A2、△A2P3A3、…均为等腰直角三角形,直角顶点P1、P2、P3、…在函数
如图,已知△OP1A1、△A1P2A2、△A2P3A3、…均为等腰直角三角形,直角顶点P1、P2、P3、…在函数

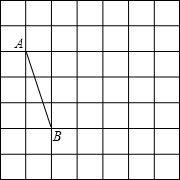 在如图所示的正方形网格中,已知线段AB,A、B均为格点.
在如图所示的正方形网格中,已知线段AB,A、B均为格点.