Question

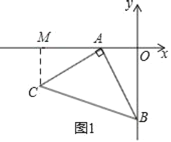
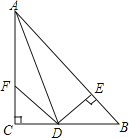
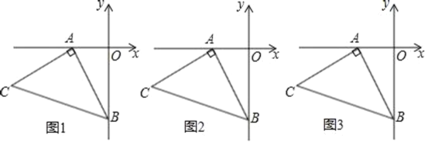
【题目】如图1，OA＝2，OB＝4，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC．

（1）求C点的坐标；

（2）如图1，在平面内是否存在一点H，使得以A、C、B、H为顶点的四边形为平行四边形？若存在，请直接写出H点坐标；若不存在，请说明理由；

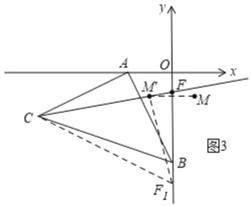
（3）如图1点M（1，﹣1）是第四象限内的一点，在y轴上是否存在一点F，使得|FM﹣FC|的值最大？若存在，请求出F点坐标；若不存在，请说明理由

Answer 1

【答案】（1）（﹣6，﹣2）;（2）见解析;（3）见解析.

【解析】

（1）证明△MAC≌△OBA（AAS），根据三角形全等时对应边相等可得C的坐标；

（2）根据平移规律可得三个H点的坐标；

（3）如图3，作点M（1，-1）关于y轴的对点M'（-1，-1），连接CF1、MF1，由于|FM-FC|≤CM，当C、M'、F三点共线时取等号，连接CM'，与y轴交于点F即为所求，根据直线解析式，令x=0可得与y轴的交点F的坐标．

解：（1）如图1，过C作CM⊥x轴于M点，

∵∠MAC+∠OAB＝90°，∠OAB+∠OBA＝90°，

则∠MAC＝∠OBA，

在△MAC和△OBA中，

，

∴△MAC≌△OBA（AAS），

∴CM＝OA＝2，MA＝OB＝4，

∴OM＝OA+AM＝2+4＝6，

∴点C的坐标为（﹣6，﹣2）

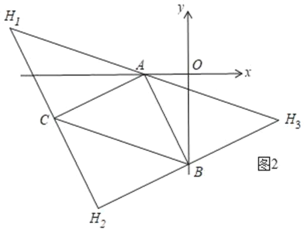
（2）答：如图2，存在三个H点，

∵A（﹣2，0），B（0，﹣4），C（﹣6，﹣2），

∴根据B到A的平移规律可得C到H1的平移规律，则H1（﹣8，2），

同理得H2（﹣4，﹣6）、H3（4，﹣2）

（3）答：存在，F（0，﹣），

如图3，作点M（1，﹣1）关于y轴的对点M'（﹣1，﹣1），

设y轴上存在一点F1，连接CF1、M'F1，由于|FM﹣FC|≤CM'，

当C、M'、F三点共线时取等号，

连接CM'，与y轴交于点F即为所求，

设CM'的解析式为：y＝kx+b，

把C（﹣6，﹣2）、M'（﹣1，﹣1）代入得，，

解得：，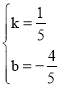

∴，

当x＝0时，y＝﹣，

∴F（0，﹣）．