题目内容
正方形ABCD,EFGH边长分别是 和
和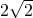 ,它们的中心O,D在直线l上,AD∥l,EG在直线l上l与DC相交于点M,ME=7-2
,它们的中心O,D在直线l上,AD∥l,EG在直线l上l与DC相交于点M,ME=7-2 ,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕Q1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕Q1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
(1)求开始运动前Q1Q2的长度;
(2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD停止旋转,求此时AE和Q1Q2的长度;
(3)两个正方形经历(2)的运动后,正方形ABCD停止旋转,正方形EFGH继续向左平移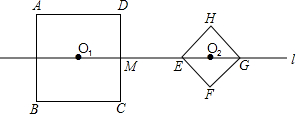 的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
解:(1)∵正方形ABCD与正方形EFGH边长分别是4和2,它们的中心O,
∴O1M= AD=
AD= ×4
×4 =2
=2 ,EG=
,EG= EH=4,
EH=4,
∴EO2= EG=2,
EG=2,
∵ME=7-2 ,
,
∴Q1Q2=O1M+ME+EO2=2 +7-2
+7-2 +2=9;
+2=9;
(2)∵正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕Q1以每秒45°顺时针方向开始旋转,
∴当两个正方形按照各自的运动方式同时运动3秒时,如图:
∴Q1Q2=9-3=6,
∵AC= AD=8,
AD=8,
∵O1A= AC=
AC= ×8=4,
×8=4,
∴AE=Q1Q2-O1A-O2E=6-4-2=0;
(3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y=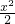 .
.
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2 )2=8.
)2=8.
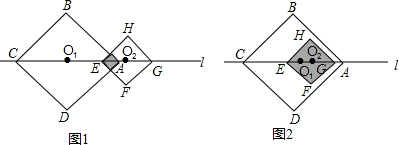
③如图3,当8≤x<12时,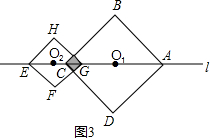
∵CG=12-x,
∴y与x之间的函数关系式为y=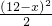 =
= x2-12x+72.
x2-12x+72.
④当x≥12时,y与x之间的函数关系式为y=0.
分析:(1)开始运动前Q1O2=O1M+ME+O2E,O1M= AD=2
AD=2  ,O2E=
,O2E= EH=2,即可求得O1O2的值.
EH=2,即可求得O1O2的值.
(2)当运动3秒后,A在直线l上,O1A= AD=4,O1E=7-3=4,因此O1E=O1A,A、E重合,即AE=0.O1O2=O1A+O2E=4+2=6.
AD=4,O1E=7-3=4,因此O1E=O1A,A、E重合,即AE=0.O1O2=O1A+O2E=4+2=6.
(3)本题要分四种情况:
①当0≤x<4时,图1,重合的小正方形对角线AE=x,因此y= x2.
x2.
②当4≤x<8时,图2,正方形EFGH在正方形ABCD内部,重合部分的面积就是正方形EFGH的面积.
③当8≤x<12时,图3,参照①的解法.
④当x≥12时,此时两正方形不重合,因此y=0.
点评:本题为运动性问题,考查了正方形的性质、图形的旋转、二次函数的应用等知识.综合性强,难度较大,解题的关键是注意分类讨论思想与数形结合的数学思想的应用.
∴O1M=
 AD=
AD= ×4
×4 =2
=2 ,EG=
,EG= EH=4,
EH=4,∴EO2=
 EG=2,
EG=2,∵ME=7-2
 ,
,∴Q1Q2=O1M+ME+EO2=2
 +7-2
+7-2 +2=9;
+2=9;(2)∵正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕Q1以每秒45°顺时针方向开始旋转,

∴当两个正方形按照各自的运动方式同时运动3秒时,如图:
∴Q1Q2=9-3=6,
∵AC=
 AD=8,
AD=8,∵O1A=
 AC=
AC= ×8=4,
×8=4,∴AE=Q1Q2-O1A-O2E=6-4-2=0;
(3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y=
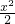 .
.②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2
 )2=8.
)2=8.
③如图3,当8≤x<12时,

∵CG=12-x,
∴y与x之间的函数关系式为y=
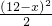 =
= x2-12x+72.
x2-12x+72.④当x≥12时,y与x之间的函数关系式为y=0.
分析:(1)开始运动前Q1O2=O1M+ME+O2E,O1M=
 AD=2
AD=2  ,O2E=
,O2E= EH=2,即可求得O1O2的值.
EH=2,即可求得O1O2的值.(2)当运动3秒后,A在直线l上,O1A=
 AD=4,O1E=7-3=4,因此O1E=O1A,A、E重合,即AE=0.O1O2=O1A+O2E=4+2=6.
AD=4,O1E=7-3=4,因此O1E=O1A,A、E重合,即AE=0.O1O2=O1A+O2E=4+2=6.(3)本题要分四种情况:
①当0≤x<4时,图1,重合的小正方形对角线AE=x,因此y=
 x2.
x2.②当4≤x<8时,图2,正方形EFGH在正方形ABCD内部,重合部分的面积就是正方形EFGH的面积.
③当8≤x<12时,图3,参照①的解法.
④当x≥12时,此时两正方形不重合,因此y=0.
点评:本题为运动性问题,考查了正方形的性质、图形的旋转、二次函数的应用等知识.综合性强,难度较大,解题的关键是注意分类讨论思想与数形结合的数学思想的应用.

练习册系列答案
相关题目
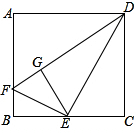 如图,将边长为2的正方形ABCD沿EF和ED折叠,使得B、C两点折叠后重合于G,则∠EFG的正切值为
如图,将边长为2的正方形ABCD沿EF和ED折叠,使得B、C两点折叠后重合于G,则∠EFG的正切值为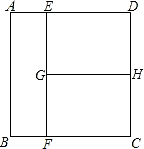 如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.
如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.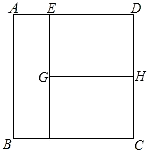 如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.
如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和. 如图,将边长为2的正方形ABCD沿EF和ED折叠,使得B、C两点折叠后重合于G,则∠EFG的正切值为________.
如图,将边长为2的正方形ABCD沿EF和ED折叠,使得B、C两点折叠后重合于G,则∠EFG的正切值为________.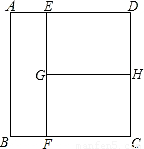 如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.
如图,单位正方形ABCD被EF、GH分成相等的矩形.试问:是否存在另外的分法,既能将单位正方形分成面积相等的三个多边形,又能使三个多边形的公共边界小于EF与GH的和.