��Ŀ����
����Ŀ����ͼ����������ABCD�У�BDΪ�Խ��ߣ���P��A������������AB�˶�������PD������D��DE��PD����ֱ��BC�ڵ�E��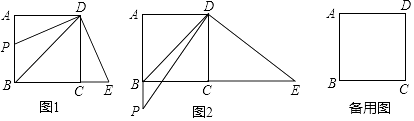
��1��̽�����֣�
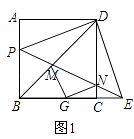
����P���߶�AB��ʱ����ͼ1����BP+CE=BD��
��2����ѧ˼����
����P���߶�AB���ӳ�����ʱ����ͼ2���������߶�BP��CE��BD֮������Ĺ�ϵʽ��������֤����
��3����չӦ�ã�
��ֱ��PE�ֱ��߶�BD��CD�ڵ�M��N��PM= ![]() ��EN=
��EN= ![]() ��ֱ��д��PD�ij���
��ֱ��д��PD�ij���
���𰸡�
��1��![]()
��2���⣺CE��BP= ![]() BD��
BD��
���ɣ��ߡ�PAD�ա�ECD��
��CE=AP��
��CE��BP=AP��BP=AB= ![]() BD��
BD��
��3���⣺�ٵ�P���߶�AB��ʱ��
��ͼ1��ʾ����BC��ȡһ��Gʹ��BG=BP������MG��NG��
�ߡ�APD�ա�CED��
��AP=CE��PD=ED��
���PED�ǵ���ֱ�������Σ�
��AB=BC=AP+BP=BG+CG��
��CG=CE��
���֤��NCG�ա�NCE��
��NG=NE����NGC=��NEC��
�ߡ�PBM=��GBM=45�㣬BP=BG��BM=BM��
���BPM�ա�BGM
��PM=GM����MGB=��MPB��
�֡�NEC+��MPB=90�㣬
���NGC+��MGB=90�㣬
���MGN=90�㣬
��MN= ![]() =2
=2 ![]() ��
��
��PE=PM+MN+EN= ![]() +2
+2 ![]() +
+ ![]() =3
=3 ![]() +
+ ![]() ��
��
��PD= ![]() PE=3+
PE=3+ ![]() ��
��
�ڵ�P��AB�ӳ�����ʱ��
��ͼ2��ʾ���ӳ�CB��G��ʹ��CG=CE������MG��NG�� 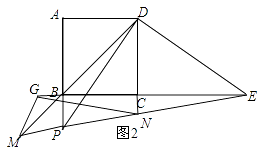
��AP=CE��
��CE��BC=CG��BC=AP��AB=BP=BG��
ͬ�ٿ�֤����BMG�ա�BMP����CNG�ա�CNE��
��PM=GM��GN=EN����BGM=��BPM=90��+��CEN=90��+CGN��
���CGN=��BGM��90��=��BGM����MGN��
���MGN=90�㣬
��MN= ![]() =2
=2 ![]() ��
��
��PN=MN��PM=2 ![]() ��
�� ![]() =
= ![]() ��
��
��PE=PN+EN= ![]() +
+ ![]() ��
��
��PD= ![]() PE=1+
PE=1+ ![]() ��
��
��PD�ij�Ϊ3+ ![]() ��1+
��1+ ![]() ��
��
��������֤������1�����ı���ABCD�������Σ�
���A=��ADC=��BCD=��DCE=90�㣬AD=CD��
��DE��PD��
���ADC=��PDE=90�㣬
���ADP=90�㩁��PDC=��CDE��
�ڡ�PAD���ECD�У� 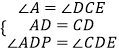 ��
��
���PAD�ա�ECD
��AP=CE��
��BP+CE=BP+AP=AB= ![]() BD��
BD��
���Դ��ǣ� ![]() ��
��
�����㾫����������Ŀ����֪���������������ε����ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�