题目内容
如图,一棵大树在一次强烈的地震中于离地面8米的A处折断倒下,树顶落在地面的C处,经测量∠ACB=30°,则大树在折断前高 米.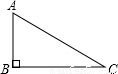
【答案】分析:在Rt△ABC中运用30°角所对的直角边等于斜边的一半,可得AC=2AB,进而求得AB+AC的值,即为原来树的高.
解答:解:如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=8米.
则AC=2AB=16米,
AB+AC=8+16=24米.
即大树折断之前高为24米.
点评:考查了勾股定理的应用,解题的关键是把实际问题转化为数学问题,抽象到直角三角形中,利用直角三角形的性质解答.
解答:解:如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=8米.
则AC=2AB=16米,
AB+AC=8+16=24米.
即大树折断之前高为24米.
点评:考查了勾股定理的应用,解题的关键是把实际问题转化为数学问题,抽象到直角三角形中,利用直角三角形的性质解答.

练习册系列答案
相关题目
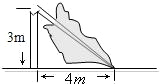 如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为
如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为 如图,一棵大树在一次强台风中于离地面3米处折断倒下,倒下后的树顶与树根的距离为4米,这棵大树在折断前的高度为
如图,一棵大树在一次强台风中于离地面3米处折断倒下,倒下后的树顶与树根的距离为4米,这棵大树在折断前的高度为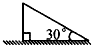 如图,一棵大树在一次强台风中于距地面5米处倒下,则这棵树在折断前的高度为
如图,一棵大树在一次强台风中于距地面5米处倒下,则这棵树在折断前的高度为 如图,一棵大树在一次强台风中于离地面3米处折断倒下,倒下树尖部分与树头距离为4米,这棵大树原来的高度为( )
如图,一棵大树在一次强台风中于离地面3米处折断倒下,倒下树尖部分与树头距离为4米,这棵大树原来的高度为( )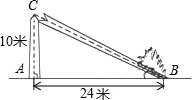 如图.一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处,大树在折断之前高为( )
如图.一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处,大树在折断之前高为( )