Question

【题目】如图，已知△ABC

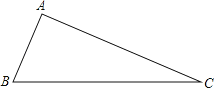
（1）用直尺和圆规，作出BC边上的中线AD（不写作法，保留作图痕迹）；

（2）若AD=BC，证明△ABC是直角三角形．

Answer 1

【答案】见解析

【解析】

试题分析：（1）作BC的垂直平分线交BC于D，连结AD，则AD为BC边上的中线；

（2）易得AD=BD=CD，则∠B=∠BAD，∠C=∠CAD，利用三角形内角和得到∠BAD+∠BAC+∠CAD=180°，则可计算出∠BAC=90°，于是可判断△ABC是直角三角形．

（1）解：如图，AD为所作；

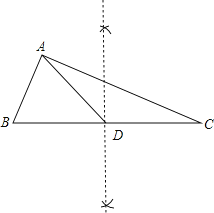
（2）证明：∵AD是BC边上的中线，且AD=BC，

∴AD=BD=CD，

∴∠B=∠BAD，∠C=∠CAD，

又∵∠B+∠BAC+∠C=180°，

∴∠BAD+∠BAC+∠CAD=180°，

即2∠BAC=180°，

∴∠BAC=90°，

即△ABC是直角三角形．