题目内容
甲、乙两人分别加工1000个零件.已知甲比乙每小时多加工20个零件,且甲加工350个零件所用的时间与乙加工250个零件所用的时间相同.(1)求甲、乙每小时各能加工多少个零件?
(2)如果要求完成这项工程的时间不超过10小时,那么如何为甲、乙两人分配工作量(甲、乙先后加工,不能同时进行加工),试列出设计方案?
【答案】分析:(1)可设甲每小时加工零件x个,表示乙每小时加工零件个数.根据甲加工350个零件所用的时间与乙加工250个零件所用的时间相同列方程解答;
(2)设分配给甲y个零件,则分配给乙(1000-y)个零件.根据加工时间列不等式组求特殊解.
解答:解:(1)设甲每小时能加工x个零件.
依题意得: ,
,
解得x=70.
经检验:x=70是原方程的根,且符合题意.
则70-20=50(个/时).
答:甲、乙两人每小时分别能加工70个和50个零件.
(2)设分配给甲y个零件,则分配给乙(1000-y)个零件.
由题意,得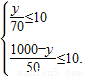 ,
,
解得500≤y≤700.
所以分配方案有3种.
方案一:分配给甲500个零件,分配给乙500个零件;
方案二:分配给甲600个零件,分配给乙400个零件;
方案三:分配给甲700个零件,分配给乙300个零件.
点评:此题考查分式方程的应用和不等式组的应用,综合性强.
(2)设分配给甲y个零件,则分配给乙(1000-y)个零件.根据加工时间列不等式组求特殊解.
解答:解:(1)设甲每小时能加工x个零件.
依题意得:
 ,
,解得x=70.
经检验:x=70是原方程的根,且符合题意.
则70-20=50(个/时).
答:甲、乙两人每小时分别能加工70个和50个零件.
(2)设分配给甲y个零件,则分配给乙(1000-y)个零件.
由题意,得
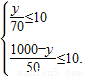 ,
,解得500≤y≤700.
所以分配方案有3种.
方案一:分配给甲500个零件,分配给乙500个零件;
方案二:分配给甲600个零件,分配给乙400个零件;
方案三:分配给甲700个零件,分配给乙300个零件.
点评:此题考查分式方程的应用和不等式组的应用,综合性强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
