题目内容
 (2012•泰州一模)如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:
(2012•泰州一模)如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:| 3 |
| 3 |
分析:由i的值求得大堤的高度AE,点A到点B的水平距离BE,从而求得MN的长度,由仰角求得DN的高度,从而由DN,AM,h求得高度CD.
解答: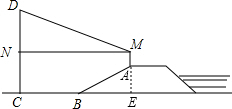 解:延长MA交直线BC于点E,
解:延长MA交直线BC于点E,
∵AB=30,i=1:
,
∴AE=15,BE=15
,
∴MN=BC+BE=30+15
,
又∵仰角为30°,
∴DN=
=
=10
+15,
CD=DN+NC=DN+MA+AE=10
+15+15+1.5≈17.32+31.5≈48.8(m).
 解:延长MA交直线BC于点E,
解:延长MA交直线BC于点E,∵AB=30,i=1:
| 3 |
∴AE=15,BE=15
| 3 |
∴MN=BC+BE=30+15
| 3 |
又∵仰角为30°,
∴DN=
| MN | ||
|
30+15
| ||
|
| 3 |
CD=DN+NC=DN+MA+AE=10
| 3 |
点评:本题考查了直角三角形在坡度上的应用,由i的值求得大堤的高度和点A到点B的水平距离,求得MN,由仰角求得DN高度,进而求得总高度.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
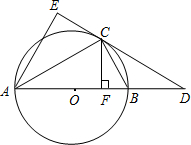 (2012•泰州一模)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(2012•泰州一模)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.