Question

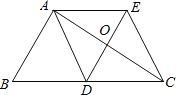
【题目】如图，AB是半圆O的直径，AB=10，C、D是半圆上两个动点，且始终保持线段CD=8．

（1）当CD∥AB时，求CD与AB之间的距离；

（2）在C、D运动的过程中，AD与BC交于点E，∠BED=α，α值是否是定值？若不是，说明理由；若是，求出tanα．

Answer 1

【答案】（1）CD与AB之间的距离是3；（2）tanα=．

【解析】

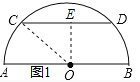
试题分析：（1）如图1，过O作OE⊥CD于E，连接OC，根据垂径定理得到CE=CD=4，根据勾股定理即可得到结论；

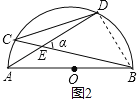
（2）α值是定值，如图2，连接BD，根据△CDE∽△ABE，求得==，于是得到cos∠α==，推出α值是定值，根据勾股定理得到BD==3k．即可的结论．

解：（1）如图1，过O作OE⊥CD于E，连接OC，

∴CE=CD=4，

∴OE==3，

∴CD与AB之间的距离是3；

（2）α值是定值，如图2，连接BD，

∵∠C=∠DAB，∠CDA=∠ABC，

∴△CDE∽△ABE，

∴==，

∵AB是半圆O的直径，

∴∠ADB=90°，

∴cos∠α==，

∴α值是定值，

设DE=4k，BE=5k，

∴BD==3k．

∴tanα===．