题目内容
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE. 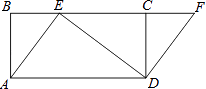
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠DCF=90°,
∵∠BAE=∠CDF,
在△ABE和△DCF中,
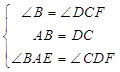 ,
,
∴△ABE≌△DCF(ASA),
∴BE=CF,
∴BC=EF,
∵BC=AD,
∴EF=AD,
又∵EF∥AD,
∴四边形AEFD是平行四边形;
(2)解:由(1)知:EF=AD=5,
在△EFD中,∵DF=3,DE=4,EF=5,
∴DE2+DF2=EF2,
∴∠EDF=90°,
∴ ![]() EDDF=
EDDF= ![]() EFCD,
EFCD,
∴CD= ![]() .
.
【解析】(1)直接利用矩形的性质结合全等三角形的判定与性质得出BE=CF,进而得出答案;(2)利用勾股定理的逆定理得出∠EDF=90°,进而得出 ![]() EDDF=
EDDF= ![]() EFCD,求出答案即可.
EFCD,求出答案即可.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 | 乙种原料 | |
维生素C含量(单位千克) | 600 | 100 |
原料价格(元千克) | 8 | 4 |
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x kg,则x应满足的不等式为( )
A.600x+100(10﹣x)≥4200
B.8x+4(100﹣x)≤4200
C.600x+100(10﹣x)≤4200
D.8x+4(100﹣x)≥4200