题目内容
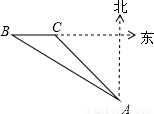
 如图,某海关缉私艇巡逻到达A处时,接到情报,在A处北偏西60°方向的B处发现一艘可疑的船只,正以24海里/小时的速度向正东方向前进,上级命令要对可疑船只进行检查,该艇立即沿北偏西45°的方向快速前进,经过一小时的航行,正好在C处截住可疑船只,则该艇的速度约为
如图,某海关缉私艇巡逻到达A处时,接到情报,在A处北偏西60°方向的B处发现一艘可疑的船只,正以24海里/小时的速度向正东方向前进,上级命令要对可疑船只进行检查,该艇立即沿北偏西45°的方向快速前进,经过一小时的航行,正好在C处截住可疑船只,则该艇的速度约为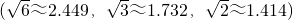 .
.
- A.44
- B.45
- C.46
- D.47
C
分析:作AD垂直于BC,交BC的延长线于D点,在Rt△ADC和Rt△ADB中,BD、CD就可以用AD表示出来,根据BC=24海里,就可以得到关于AD的方程,解方程,就可以求出AD.进而求出AC,得到该艇的速度.
解答:作AD垂直于BC,交BC的延长线于D点,在Rt△ADC中,∠DAC=45°
∴设AD=DC=x(海里),则AC= x海里?
x海里?
在Rt△ADB中,∠ADB=90°,∠DAB=60°
∴∠B=30°
∴BD= AD
AD
即24+x= x
x
∴x=12( +1)?
+1)?
∴AC=12( +1)•
+1)• =12
=12 +12
+12 ≈46(海里)
≈46(海里)
∴V=46(海里/时).
故选:C.
点评:此题考查的知识点是解直角三角形的应用,关键是解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
分析:作AD垂直于BC,交BC的延长线于D点,在Rt△ADC和Rt△ADB中,BD、CD就可以用AD表示出来,根据BC=24海里,就可以得到关于AD的方程,解方程,就可以求出AD.进而求出AC,得到该艇的速度.
解答:作AD垂直于BC,交BC的延长线于D点,在Rt△ADC中,∠DAC=45°

∴设AD=DC=x(海里),则AC=
 x海里?
x海里?在Rt△ADB中,∠ADB=90°,∠DAB=60°
∴∠B=30°
∴BD=
 AD
AD即24+x=
 x
x∴x=12(
 +1)?
+1)?∴AC=12(
 +1)•
+1)• =12
=12 +12
+12 ≈46(海里)
≈46(海里)∴V=46(海里/时).
故选:C.
点评:此题考查的知识点是解直角三角形的应用,关键是解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
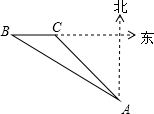 如图,某海关缉私艇巡逻到A处时接到情报,在A处北偏西60°方向的B处发现一艘可疑船只正向正东方向前进,上级命令要对可疑船只进行检查,该艇立即以每小时48海里的速度沿北偏西45°的方向前进,经过1小时的航行恰好在C处截住可疑船只,求该可疑船只的速度.(结果保留整数,
如图,某海关缉私艇巡逻到A处时接到情报,在A处北偏西60°方向的B处发现一艘可疑船只正向正东方向前进,上级命令要对可疑船只进行检查,该艇立即以每小时48海里的速度沿北偏西45°的方向前进,经过1小时的航行恰好在C处截住可疑船只,求该可疑船只的速度.(结果保留整数,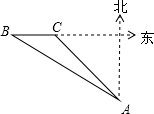 如图,某海关缉私艇巡逻到A处时接到情报,在A处北偏西60°方向的B处发现一艘可疑船只正向正东方向前进,上级命令要对可疑船只进行检查,该艇立即以每小时48海里的速度沿北偏西45°的方向前进,经过1小时的航行恰好在C处截住可疑船只,求该可疑船只的速度.(结果保留整数,
如图,某海关缉私艇巡逻到A处时接到情报,在A处北偏西60°方向的B处发现一艘可疑船只正向正东方向前进,上级命令要对可疑船只进行检查,该艇立即以每小时48海里的速度沿北偏西45°的方向前进,经过1小时的航行恰好在C处截住可疑船只,求该可疑船只的速度.(结果保留整数,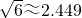 ,
,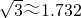 ,
,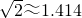 .)
.)
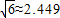 ,
,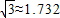 ,
,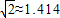 .)
.)