题目内容
一个凸多边形的某一个内角的外角与其余内角的和恰为500°,那么这个多边形的边数是________或________.
4 5
分析:本题涉及多边形的内角和、方程的思想.关键是根据内角和的公式和等量关系“一个凸多边形的某一个内角的外角与其余内角的和恰为500°”列出方程,挖掘隐含着边数为正整数这个条件求解.
解答:设边数为n,这个内角为x度,则0<x<180°根据题意,得
(n-2)•180°-x+(180°-x)=500°
解得n=3+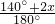 .
.
∵n为正整数,
∴140+2x必为180的倍数,
又∵0<x<180,
∴n=4或5.
故答案为:4,5.
点评:主要考查了多边形的内角和定理及内角与外角的关系,较难.
n边形的内角和为:180°•(n-2);多边形的内角与它的外角互为邻补角.
分析:本题涉及多边形的内角和、方程的思想.关键是根据内角和的公式和等量关系“一个凸多边形的某一个内角的外角与其余内角的和恰为500°”列出方程,挖掘隐含着边数为正整数这个条件求解.
解答:设边数为n,这个内角为x度,则0<x<180°根据题意,得
(n-2)•180°-x+(180°-x)=500°
解得n=3+
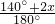 .
.∵n为正整数,
∴140+2x必为180的倍数,
又∵0<x<180,
∴n=4或5.
故答案为:4,5.
点评:主要考查了多边形的内角和定理及内角与外角的关系,较难.
n边形的内角和为:180°•(n-2);多边形的内角与它的外角互为邻补角.

练习册系列答案
相关题目