题目内容
已知l是⊙O的切线,⊙O的直径AB=10cm,那么点A、B到直线l的距离之和为________cm.
10
分析:根据题意画出图形,如图所示,当AB与l不平行时,分别过点A和点B作直线l的垂线,AC+BD即为所求的距离之和,连接OE,根据切线性质得到OE垂直于直线l,进而得到四边形ABDC为梯形,根据梯形中位线定理和直径AB的长度即可求出距离之和;当AB与l平行时,显然距离之和等于直径AB的长.
解答: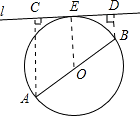 解:根据题意画出图形,如图所示,设直线l与圆的切点为E,
解:根据题意画出图形,如图所示,设直线l与圆的切点为E,
过A作AC⊥l,垂足为C,过B作BD⊥l,垂足为D,连接OE,则OE⊥l,
当AB不平行l时,四边形ABDC为梯形,又O为AB的中点,∴OE为梯形的中位线,
∴OE= (AC+BD),即AC+BD=2OE=AB=10cm,
(AC+BD),即AC+BD=2OE=AB=10cm,
当AB∥l时,四边形ABDC为矩形,AC+BD=AB=10cm,
综上,点A、B到直线l的距离之和为10cm.
故答案为:10.
点评:此题考查学生掌握切线的性质以及梯形中位线的性质,考查了数形结合及分类讨论的数学思想,是一道中档题.以后做题注意已知切线连接圆心与切点是经常连接的辅助线.
分析:根据题意画出图形,如图所示,当AB与l不平行时,分别过点A和点B作直线l的垂线,AC+BD即为所求的距离之和,连接OE,根据切线性质得到OE垂直于直线l,进而得到四边形ABDC为梯形,根据梯形中位线定理和直径AB的长度即可求出距离之和;当AB与l平行时,显然距离之和等于直径AB的长.
解答:
 解:根据题意画出图形,如图所示,设直线l与圆的切点为E,
解:根据题意画出图形,如图所示,设直线l与圆的切点为E,过A作AC⊥l,垂足为C,过B作BD⊥l,垂足为D,连接OE,则OE⊥l,
当AB不平行l时,四边形ABDC为梯形,又O为AB的中点,∴OE为梯形的中位线,
∴OE=
 (AC+BD),即AC+BD=2OE=AB=10cm,
(AC+BD),即AC+BD=2OE=AB=10cm,当AB∥l时,四边形ABDC为矩形,AC+BD=AB=10cm,
综上,点A、B到直线l的距离之和为10cm.
故答案为:10.
点评:此题考查学生掌握切线的性质以及梯形中位线的性质,考查了数形结合及分类讨论的数学思想,是一道中档题.以后做题注意已知切线连接圆心与切点是经常连接的辅助线.

练习册系列答案
相关题目
已知PA是⊙O的切线,A为切点,PBC是割线,且AC是⊙O的直径,若PA=4,BC=6,则sin∠P的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
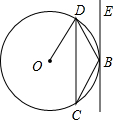 如图,已知BE是⊙O的切线,点C、D在⊙O上,∠DCB=40°,则∠EBD=
如图,已知BE是⊙O的切线,点C、D在⊙O上,∠DCB=40°,则∠EBD=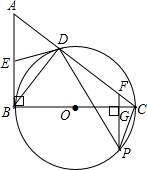 (2012•东莞模拟)如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F
(2012•东莞模拟)如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F