题目内容
某公司销售一种新型产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=-
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).
(1)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(2)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(3)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
| 1 |
| 100 |
| 1 |
| 100 |
(1)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(2)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(3)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
分析:(1)根据“利润=销售额-成本-广告费”可求出w内与x间的函数关系式,根据“利润=销售额-成本-附加费”可求出w外与x间的函数关系式;
(2)先运用二次函数的性质求出w内取最大值时x的值,再根据w外的最大值等于w内的最大值,列出关于a的方程,解方程即可求出a的值;
(3)先分别求出当x=5000时,w内与w外的值,再分w内<w外,w内=w外,w内>w外这三种情况进行讨论,即可求出a的取值范围.
(2)先运用二次函数的性质求出w内取最大值时x的值,再根据w外的最大值等于w内的最大值,列出关于a的方程,解方程即可求出a的值;
(3)先分别求出当x=5000时,w内与w外的值,再分w内<w外,w内=w外,w内>w外这三种情况进行讨论,即可求出a的取值范围.
解答:解:(1)w内=x(y-20)-62500=x(-
x+150-20)-62500=-
x2+130x-62500,
即w内=-
x2+130x-62500,
w外=x(150-a)-
x2=-
x2+(150-a)x,
即w外=-
x2+(150-a)x;
(2)∵w内=-
x2+130x-62500,
∴当x=-
=6500时,w内最大;
∵在国外销售月利润的最大值与在国内销售月利润的最大值相同,
∴
=
,
整理,得(150-a)2=14400,
解得a1=30,a2=270(不合题意,舍去).
∴a=30.
(3)当x=5000时,w内=-
×50002+130×5000-62500=337500,
w外=-
×50002+(150-a)×5000=-5000a+500000.
若w内<w外,即当a<32.5时,在国外销售才能使所获月利润较大;
若w内=w外,即当a=32.5时,在国内、外销售所获月利润一样大;
w内>w外,即当a>32.5时,在国内销售才能使所获月利润较大.
| 1 |
| 100 |
| 1 |
| 100 |
即w内=-
| 1 |
| 100 |
w外=x(150-a)-
| 1 |
| 100 |
| 1 |
| 100 |
即w外=-
| 1 |
| 100 |
(2)∵w内=-
| 1 |
| 100 |
∴当x=-
| 130 | ||
2×(-
|
∵在国外销售月利润的最大值与在国内销售月利润的最大值相同,
∴
| 0-(150-a)2 | ||
4×(-
|
4×(-
| ||
4×(-
|
整理,得(150-a)2=14400,
解得a1=30,a2=270(不合题意,舍去).
∴a=30.
(3)当x=5000时,w内=-
| 1 |
| 100 |
w外=-
| 1 |
| 100 |
若w内<w外,即当a<32.5时,在国外销售才能使所获月利润较大;
若w内=w外,即当a=32.5时,在国内、外销售所获月利润一样大;
w内>w外,即当a>32.5时,在国内销售才能使所获月利润较大.
点评:本题考查了二次函数在实际生活中的应用,难度适中,根据利润的关系式分别写出w内,w外与x间的函数关系式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳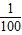 x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).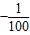 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳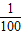 x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费). x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费). x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元),(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元),(利润=销售额-成本-附加费).