Question

【题目】如图所示，在矩形ABCD中，AB=6，AD=8，P是AD上的动点，PE⊥AC，PF⊥BD于F，则PE+PF的值为 ．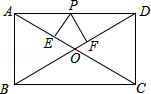

Answer 1

【答案】
【解析】解：连接OP，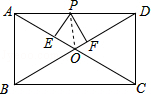
∵四边形ABCD是矩形，
∴∠DAB=90°，AC=2AO=2OC，BD=2BO=2DO，AC=BD，
∴OA=OD=OC=OB，
∴S△AOD=S△DOC=S△AOB=S△BOC= S矩形ABCD= ×6×8=12，
在Rt△BAD中，由勾股定理得：BD= = =10，
∴AO=OD=5，
∵S△APO+S△DPO=S△AOD ，
∴ ×AO×PE+ ×DO×PF=12，
∴5PE+5PF=24，
PE+PF= ，
所以答案是： ．
【考点精析】认真审题，首先需要了解矩形的性质(矩形的四个角都是直角，矩形的对角线相等)．