题目内容
已知A、B是抛物线y=x2+2x-1上的两点(A在B的左侧),且AB与x轴平行,AB=4,则点A的坐标为分析:先求出已知抛物线的对称轴和抛物线与X轴的交点C、D的坐标,利用CD和AB的大小判断出A,B在X轴的上方,根据抛物线的对称性确定出A点的横坐标,代入解析式即可求出A的纵坐标,代入即可.
解答:解:y=x2+2x-1,
-
=-
=-1,
对称轴是直线x=-1,
当y=0时,x2+2x-1=0,
解得:x1=-1+
,x2=-1-
,
x1-x2=2
,
∵a=1,开口向上,
设抛物线y=x2+2x-1于x轴交于C、D,
则CD=2
<4,
∴点A、B在x轴的上方,且关于抛物线的对称轴对称,
设AB交对称轴于M,则AM=BM=2,
∵已知A在B的左侧,
∴A点的横坐标是:-3,
把x=-3代入抛物线y=x2+2x-1得:y=2,
所以点A的坐标是(-3,2).
故答案为:(-3,2).
-
| b |
| 2a |
| 2 |
| 2×1 |
对称轴是直线x=-1,
当y=0时,x2+2x-1=0,
解得:x1=-1+
| 2 |
| 2 |
x1-x2=2
| 2 |
∵a=1,开口向上,
设抛物线y=x2+2x-1于x轴交于C、D,
则CD=2
| 2 |
∴点A、B在x轴的上方,且关于抛物线的对称轴对称,
设AB交对称轴于M,则AM=BM=2,
∵已知A在B的左侧,
∴A点的横坐标是:-3,
把x=-3代入抛物线y=x2+2x-1得:y=2,
所以点A的坐标是(-3,2).
故答案为:(-3,2).
点评:本题主要考查了二次函数的性质,一元二次方程的解法等知识,利用抛物线的对称性正确求出A的横坐标是解此题的关键,注意应先确定点A B的位置.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
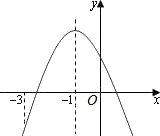 如图,已知直线x=-1是抛物线y=ax2+bx+c(a≠0)的对称轴,则①abc、②a-b+c、③a+b+c、④2a-b、⑤3a-b,其中是负数的有( )
如图,已知直线x=-1是抛物线y=ax2+bx+c(a≠0)的对称轴,则①abc、②a-b+c、③a+b+c、④2a-b、⑤3a-b,其中是负数的有( )