题目内容
(2012•北塘区一模)某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:

(1)问师生何时回到学校?
(2)如果运送工具的三轮车比师生迟半小时出发,与师生同路匀速前进,早半个小时到达植树地点,请在图中,画出该三轮车离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求13时至14时之间返回学校,往返平均速度分别为每小时8km、6km.试通过计算说明植树点选在距离学校多远较为合适.

(1)问师生何时回到学校?
(2)如果运送工具的三轮车比师生迟半小时出发,与师生同路匀速前进,早半个小时到达植树地点,请在图中,画出该三轮车离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求13时至14时之间返回学校,往返平均速度分别为每小时8km、6km.试通过计算说明植树点选在距离学校多远较为合适.
分析:(1)设直线AB的解析式为s=kt+b,然后利用待定系数法确定其解析式得s=-5t+68,再求出C点坐标即可得到师生回到学校的时间;
(2)根据题意三轮车离校路程s与时间t之间的图象过点(8.5,0)、(9.5,8),然后连接这两点的线段即可得到三轮车离校路程s与时间t之间的图象,观察图象得到此时三轮车追上师生时离学校的路程为4kn;
(3)根据题意得师生骑自行车往返所用的时间在3小时至4小时之间,设植树点在距离学校xkm,得到3≤
+
≤4,解得
≤x≤
.
(2)根据题意三轮车离校路程s与时间t之间的图象过点(8.5,0)、(9.5,8),然后连接这两点的线段即可得到三轮车离校路程s与时间t之间的图象,观察图象得到此时三轮车追上师生时离学校的路程为4kn;
(3)根据题意得师生骑自行车往返所用的时间在3小时至4小时之间,设植树点在距离学校xkm,得到3≤
| x |
| 8 |
| x |
| 6 |
| 72 |
| 7 |
| 96 |
| 7 |
解答:解:(1)如图,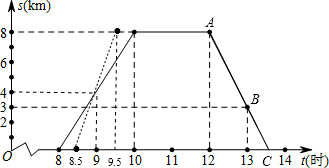
设直线AB的解析式为s=kt+b,
把A(12,8),B(13,3)分别代入得
,
解得
,
∴直线AB的解析式为s=-5t+68,
令s=0,则-5t+68=0,
解得t=13.6,
∴C点坐标为(13.6,0),
∴师生13.6时回到学校;
(2)∵三轮车比师生迟半小时出发,与师生同路匀速前进,早半个小时到达植树地点,
∴连接点(8.5,0)和(9.5,8)所得得线段为该三轮车离校路程s与时间t之间的图象,
三轮车追上师生时离学校的路程为4km;
(3)师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求13时至14时之间返回学校,则师生骑自行车往返所用的时间在3小时至4小时之间,
设植树点在距离学校xkm,
∴3≤
+
≤4,解得
≤x≤
,
∴植树点选在距离学校在
km至
km之间较为合适.

设直线AB的解析式为s=kt+b,
把A(12,8),B(13,3)分别代入得
|
解得
|
∴直线AB的解析式为s=-5t+68,
令s=0,则-5t+68=0,
解得t=13.6,
∴C点坐标为(13.6,0),
∴师生13.6时回到学校;
(2)∵三轮车比师生迟半小时出发,与师生同路匀速前进,早半个小时到达植树地点,
∴连接点(8.5,0)和(9.5,8)所得得线段为该三轮车离校路程s与时间t之间的图象,
三轮车追上师生时离学校的路程为4km;
(3)师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求13时至14时之间返回学校,则师生骑自行车往返所用的时间在3小时至4小时之间,
设植树点在距离学校xkm,
∴3≤
| x |
| 8 |
| x |
| 6 |
| 72 |
| 7 |
| 96 |
| 7 |
∴植树点选在距离学校在
| 72 |
| 7 |
| 96 |
| 7 |
点评:本题考查了一次函数的应用:先把实际问题中的数据与坐标系中的数据对应起来,利用待定系数法确定一次函数的解析式,然后利用一次函数的性质解决问题.也考查了观察函数图象的能力.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目

 (2012•北塘区一模)如图,把一个长方形的纸片对折两次,然后剪下一个角,正好得到一个完整的菱形.要使得这个菱形的一个锐角为60°,则剪口与折痕所成的角α的度数应为
(2012•北塘区一模)如图,把一个长方形的纸片对折两次,然后剪下一个角,正好得到一个完整的菱形.要使得这个菱形的一个锐角为60°,则剪口与折痕所成的角α的度数应为