Question

【题目】如图，Rt△ABC中，∠ACB＝90°, BC＝3cm, CD⊥AB于D, 在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F，若EF＝5cm，求AE.

Answer 1

【答案】2cm

【解析】试题分析：根据垂直的定义得到∠FEC=90°，∠ADF=90°，再根据等角的余角相等得到∠A=∠F，则可根据“AAS”可判断△ACB≌△FEC，所以AC=EF=5cm，然后利用AE=AC-EC进行计算即可．

试题解析：∵EF⊥AC，∴∠FEC=90°，∴∠F+∠FCE=90°，

∵CD⊥AB，∴∠ADC=90°，∴∠A+∠ACD=90°，∴∠A=∠F，

在△ACB和△FEC中 ，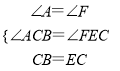

∴△ACB≌△FEC（AAS），

∴AC=EF=5cm，

又EC=BC=3cm，

∴AE=5cm-3cm=2cm．