题目内容
下列线段不能组成直角三角形的是( )．
A. a＝6，b＝8，c＝10 B. a=1，b=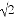
，c=
C. a=
，b=1，c=
D. a=2，b=3，c=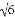
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
新课标快乐提优暑假作业陕西旅游出版社系列答案暑假衔接培优教材浙江工商大学出版社系列答案欣语文化快乐暑假沈阳出版社系列答案题目内容
下列线段不能组成直角三角形的是( )．
A. a＝6，b＝8，c＝10 B. a=1，b=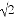，c=
C. a=，b=1，c= D. a=2，b=3，c=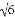
新课标快乐提优暑假作业陕西旅游出版社系列答案暑假衔接培优教材浙江工商大学出版社系列答案欣语文化快乐暑假沈阳出版社系列答案
，则
，则
；按照同样的方法继续操作下去……，第
=______________．
甲由于看错了方程（1）中的a，得到方程组的解为
，乙由于看错了方程(2)中的b，得到方程组的解为
，若按正确的计算，求x＋6y的值.