题目内容
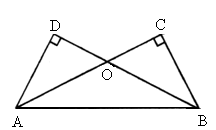
如图，已知AD⊥BD，AC⊥BC，E为AB的中点，则△CDE一定是
- A.直角三角形
- B.等腰直角三角形
- C.等腰三角形
- D.等边三角形
C
分析：根据直角三角形斜边上的中线的性质可得DE=
AB，CE=AB，可得DE=CE，再根据等腰三角形的判定进行选择．
解答：∵AD⊥BD，AC⊥BC，E为AB的中点，
∴DE=AB，CE=AB，
∴DE=CE，
∴△CDE一定是等腰三角形．
故选C．
点评：考查了直角三角形斜边上的中线的性质，等腰三角形的判定，将AB作为纽带，得到DE=CE是解题的关键．
分析：根据直角三角形斜边上的中线的性质可得DE=
AB，CE=AB，可得DE=CE，再根据等腰三角形的判定进行选择．解答：∵AD⊥BD，AC⊥BC，E为AB的中点，
∴DE=
AB，CE=AB，∴DE=CE，
∴△CDE一定是等腰三角形．
故选C．
点评：考查了直角三角形斜边上的中线的性质，等腰三角形的判定，将AB作为纽带，得到DE=CE是解题的关键．
练习册系列答案
相关题目
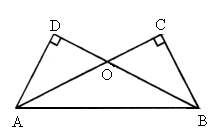
如图，已知AD⊥BD，AC⊥BC，E为AB的中点，则△CDE一定是（ ）
如图，已知AD⊥BD，AC⊥BC，D，C分别是垂足，E为AB的中点，则△CDE一定是（ ）
如图，已知AD⊥BD，AC⊥BC，∠1=25°，∠2的度数为
